« Ensemble de Mandelbrot et autres fractales » : différence entre les versions
| Ligne 66 : | Ligne 66 : | ||
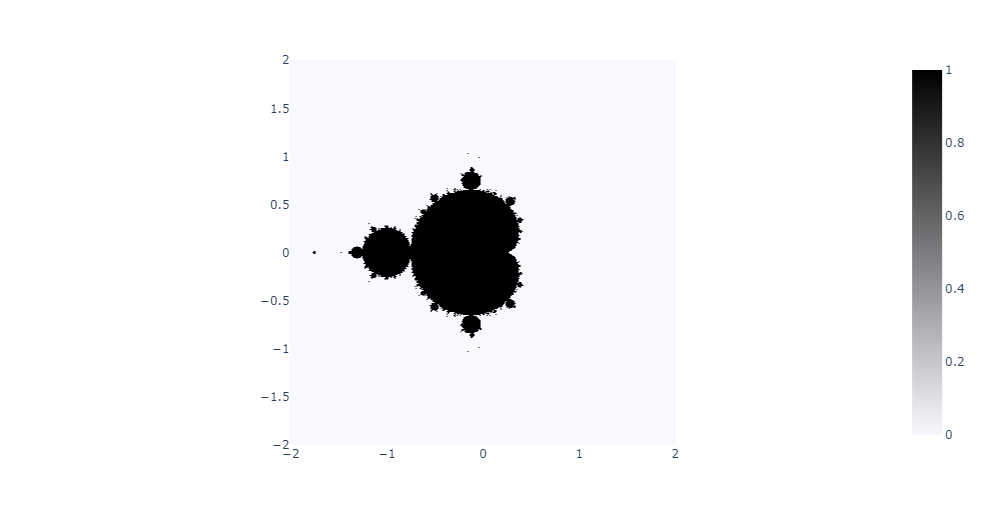
[[Fichier : newplot_(9).png|800px|thumb|none|Exemple de l'ensemble de Mandelbrot pour 100 itérations, ModuleMax = 2, de -2 à 2 en x et y]] |
[[Fichier : newplot_(9).png|800px|thumb|none|Exemple de l'ensemble de Mandelbrot pour 100 itérations, ModuleMax = 2, de -2 à 2 en x et y]] |
||
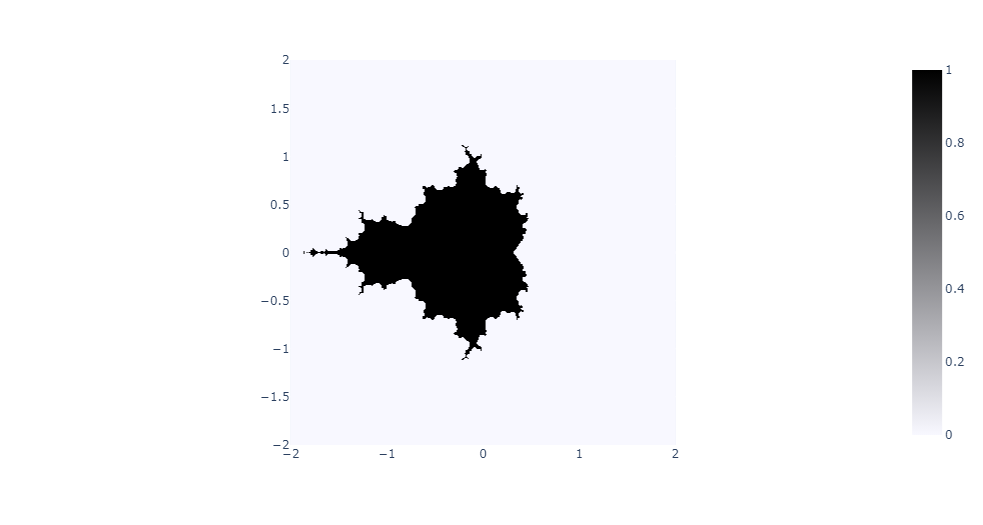
[[Fichier : newplot_(10).png|800px|thumb|none|Autre exemple de l'ensemble de Mandelbrot avec les mêmes paramètres mais 10 itérations.]] |
[[Fichier : newplot_(10).png|800px|thumb|none|Autre exemple de l'ensemble de Mandelbrot avec les mêmes paramètres mais 10 itérations.]] |
||
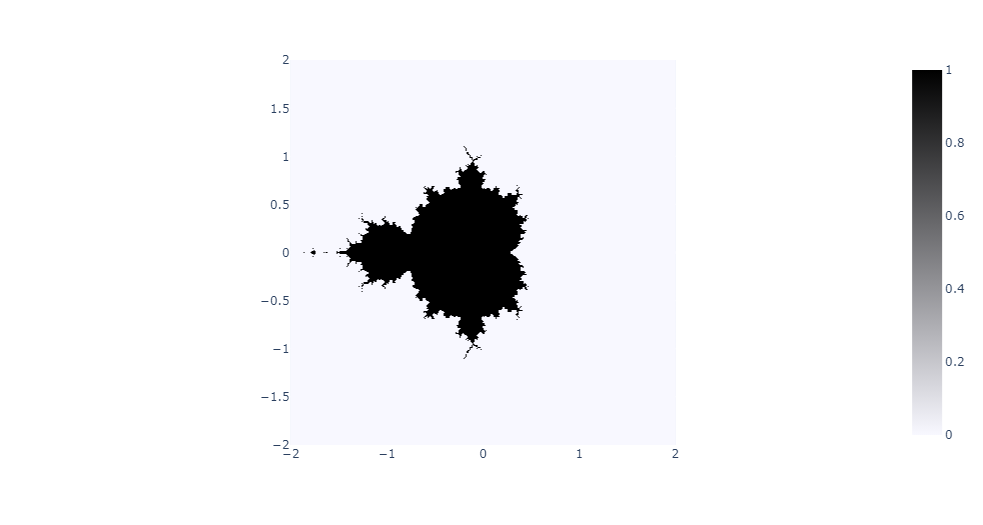
[[Fichier : newplot_(11).png|800px|thumb|none|Même chose pour 15 itérations]] |
|||
==Optimisations== |
==Optimisations== |
||
Version du 5 mai 2021 à 16:43
Qu'est ce que l'ensemble de Mandelbrot ?
L'ensemble de Mandelbrot est une fractale, c'est-à-dire une figure mathématique identique à toutes les échelles. Cet ensemble fut découvert par Gaston Julia et Pierre Fatou avant la Première Guerre Mondiale. Son nom vient du mathématicien polono-franco-américain Benoît Mandelbrot, qui réalisa les premières représentations de l'ensemble dans les années 1980. Les différents points de l'ensemble correspondent aux points des ensembles de Julia connexes, qui sont des ensembles différents pour chaque point du plan complexe.
L'ensemble de Mandelbrot est régi par une formule mathématique simple : zn+1 = zn * zn + c, où zn est un nombre complexe évoluant avec le temps et c un point complexe constant. Pour savoir si un point appartient à l'ensemble de Mandelbrot ou non, on répète ce calcul un certain nombre de fois, puis on calcule le module du point complexe obtenu. S'il est strictement inférieur à 2, le point appartient à l'ensemble. Au début du calcul pour un point complexe donnée, zn et c sont égaux.
Programme naïf en python
Le programme dit "naïf" est un programme qui est le plus "évident" possible, c'est-à-dire sans optimisations.
def intervalle(min, max, nbInter):
"""Renvoie des tableaux contenant des valeurs pour x et y
En entrée : min et max, les limites de l'espace et nbInter, le nombre de découpages voulus sur l'intervalle min-max
En sortie : deux tableaux, tabx et taby, contenant les différentes valeurs de x et y selon le découpage"""
inter = (max-min)/(nbInter-1)
tab = [min]*(nbInter)
for i in range (0,nbInter):
tab[i] = min + (inter*i)
return tab
Ici, on calcule un tableau qui sert pour les axes du graphe ainsi qu'au calcul des différents points du plan complexe.
def Mandelbrot(x,y,nbIteration,ModuleMax):
"""Indique si un nombre complexe fait partie de l'ensemble de Mandelbrot ou non
En entrée : x et y, deux coordonées, nbIteration, le nombre de répétitions de la formule et ModuleMax, le module à ne pas dépasser
En sortie : un entier, indiquant si le complexe appartient à l'ensemble ou non """
nombre = x+(y*1j)
i = 1
z = nombre
c = nombre
appartient = True
while i <= nbIteration and appartient==True :
#print(z)
#print("i ="+str(i))
if abs(z)>ModuleMax :
appartient = False
#print(abs(z))
z = (z*z)+c
i += 1
return int(appartient)
Cette fonction est la fonction de calcul des points. Pour un nombre d'itérations donné et un module maximum à ne pas dépasser, la fonction se répète et retourne le nombre d'itérations qu'il a fallu pour que le module du nombre complexe dépasse le ModuleMax. Si le nombre d'itérations obtenu est égal au nombre d'itérations donné en paramètre, le point complexe fait partie de l'ensemble.
def ensembleMandelbrot(Xmin,Xmax,Ymin,Ymax,largeur,hauteur,nbIteration,ModuleMax):
"""Retourne le tableau permettant d'afficher l'ensemble de Mandelbrot
En entrée : min et max, les bornes, nbInter, le nombre de découpages voulus, nbIteration, le nombre de répétitions et ModuleMax, le module à ne pas dépasser
En sortie : trois tableaux, le tableau des x, le tableau des y, et le tableau d'affichage de l'ensemble de Mandelbrot"""
tabx = intervalle(Xmin,Xmax,largeur)
taby = intervalle(Ymin,Ymax,hauteur)
img_nb = [[0]*len(taby) for i in range (len(tabx))]
for j in range (len(taby)):
for i in range (len(tabx)):
img_nb[len(tabx)-1-j][i] = Mandelbrot(tabx[i],taby[j],nbIteration,ModuleMax)
return (tabx, taby, img_nb)
Ceci est la fonction principale, celle qui automatise tout le processus. A chaque tour de boucle, un point complexe est sélectionné avec les tableaux de coordonnées x et y. Ce point est soumis à la fonction de calcul et le nombre d'itérations qui en ressort est stocké dans un tableau qui servira à l'affichage. A la fin de la fonction, on retourne les tableaux de coordonnées x et y, ainsi que le tableau des itérations img_nb.
def afficheMandelbrot(tab,tab2,tab3):
fig = px.imshow(tab,origin="lower",color_continuous_scale=["#F8F8FF","#000000"],x=tab2,y=tab3)
fig.show()
Enfin cette fonction permet d'afficher l'ensemble de Mandelbrot avec la bibliothèque plotly. On fournit d'abord le tableau correspondant aux différents points calculés, l'origine du repère, les deux couleurs (blanc et noir), ainsi que les axes avec les tableaux de coordonnées x et y.