« Origami, axiomes de Huzita/Justin et ReferenceFinder » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| Ligne 12 : | Ligne 12 : | ||
=== Axiome 1 === |
=== Axiome 1 === |
||
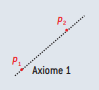
Étant donnés deux points p1 et p2, il existe un seul pli qui passe par ces deux-là. [[ |
Étant donnés deux points p1 et p2, il existe un seul pli qui passe par ces deux-là. [[Fichier:Axiome_1.png|200px|thumb|left|texte descriptif]] |
||
Version du 21 mai 2022 à 10:28
L'origami est un art du pliage de papier pour en faire une sculpture, soit géométrique, par exemple une boîte, soit figurative, comme un animal, une fleur, un personnage, etc... qui fut inventé en Chine au 6ème siècle. Depuis la création des ordinateurs, et de programmes dediés à ceux-ci, comme le programme ReferenceFinder, qui utilise les axiomes de Justin-Huzita-Hatori, le pliage de papier est une science qui a été développée virtuellement. L'origami est une science très puissante qui nous permet de faire des choses impossible avec seulement une règle et un compas. L'approfondissement de la géométrie peut se faire à travers le pliage de papier, grâçe aux nouvelles théories créées par celui-ci
Les machines de nos jours nous facilitent la création d'origamis, à travers de nombreux calculs de droites et de points dans un plan.
Les axiomes de Justin-Huzita-Hatori
Ces axiomes ont été inventées par un groupe de 3 personnes : Jacques Justin, Humaki Huzita et Koshiro Hatori. Ils se sont demandés comment trouver tous les plis possibles et inimaginables sur une feuille de papier, en fonction de droites et de points sur celle-ci.
Les axiomes sont au nombre de 7, les 4 premiers étants plutôt basiques et facilement compréhensibles, jusqu'au dernier axiome consistant à résoudre des équations du 3ème degré pour trouver un pli, grace à plusieurs droites et points, et des opérations de perpendicularité ou de parallélisme entre les uns et les autres.
Axiome 1
Étant donnés deux points p1 et p2, il existe un seul pli qui passe par ces deux-là.