Simulation de fluides

Tuteur: Colin Weill-Duflos

Etudiant : Rousseau Maxime

Lorsque l'on veut afficher de l'eau sur un écran, on veut généralement représenter son mouvement sans qu'un animateur n'ait à préciser à la main le déplacement de chaque polygone représentant la surface de l'eau. Pour cela, on emploie des modélisation physiques du fluide pour simuler son comportement, puis on effectue un rendu du fluide ainsi modélisé. Les modèles physiques employés pour simuler un fluide sont complexes et font apparaître des phénomènes comme des vortex, des vagues... Il faut donc des méthodes de simulation fines capturant la complexité de ces phénomènes.

Introduction: affichage, schéma d’Euler

On utilisera python, avec la bilbiothèque numpy pour créer et manipuler des tableaux, et matplotlib pour afficher des choses.

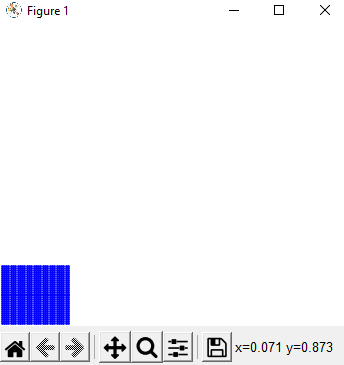
Commencer par afficher une grille 30x30 en 2d de particules (des points), occupant un coin de l’écran.

Simulation d’un modèle physique simple

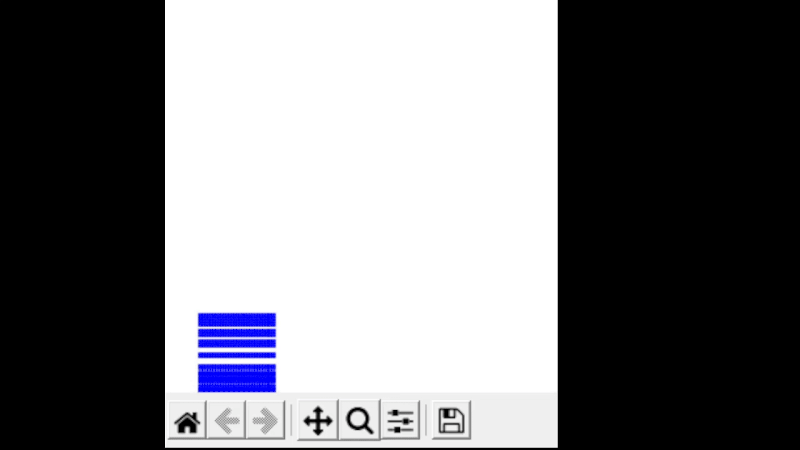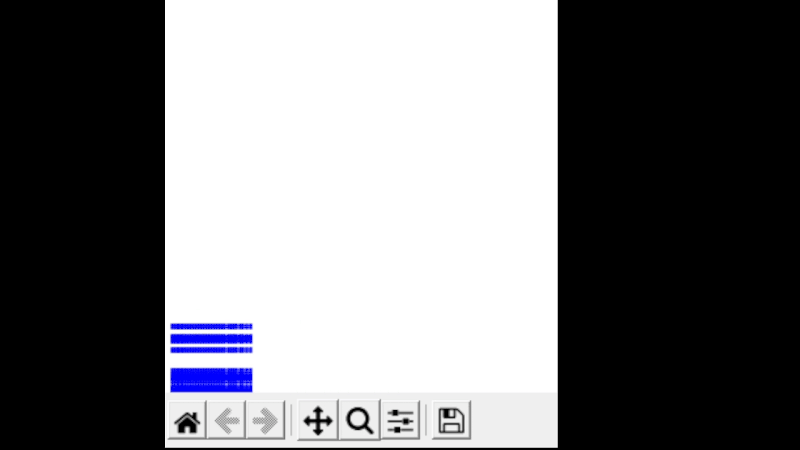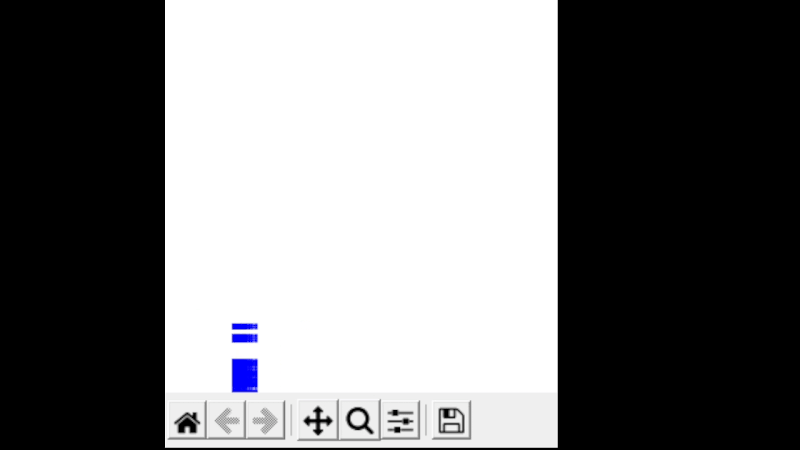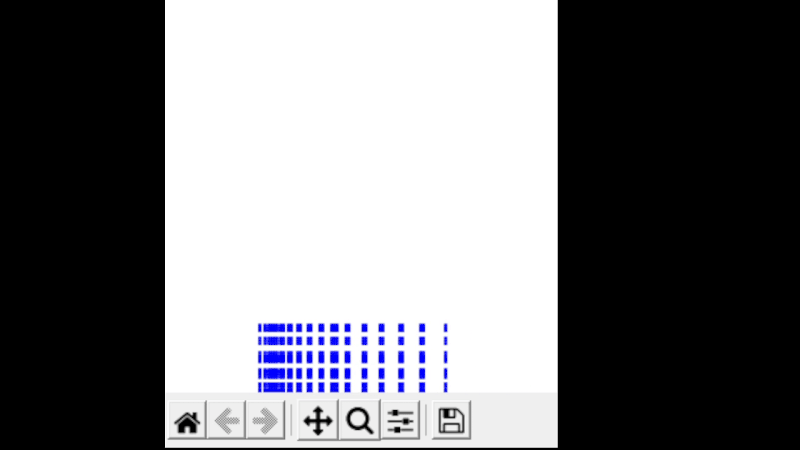
Commençons par simuler la chute de chaque particule comme si celle-ci étaient juste des masses en chute libre.

Construire un tableau pour la position de chaque particule (si ce n’est pas déjà fait), la vitesse et l’accélération. Initialiser la position pour avoir la même grille qu’avant, et la vitesse ainsi que l’accélération à 0. Puisque l’on est en 2 dimensions, on peut choisir de représenter position, vitesse, accélération comme des tableaux à 2 dimensions ou bien deux tableaux chacun.

On suppose que chaque particule est soumise à un la gravité. Rajouter une boucle dans laquelle:

- on fait avancer une variable de temps t d’un pas de temps dt

- on actualise la valeur de l’accélération, puis la vitesse à partir de l’accélération à partir de la position

- on actualise l’affichage avec les nouvelles positions des particules

Pour calculer la vitesse en fonction de l’accélération, et la position en fonction de la vitesse, on se rappelle d’abord le lien entre chaque grandeur, puis on utilise la méthode d’Euler explicite. ( https://fr.wikipedia.org/wiki/Méthode_d%27Euler )

Conditions aux bords

Rajouter des contraintes au bord, simulant un rebond. Chaque particule devrait rebondir jusqu’à sa position initialie. Rajouter une vitesse initiale horizontale non nulle, afin de vérifier que le rebond fonctionne bien sur tous les bords.

On a à présent les conditions aux bords ainsi que la boucle d’actualisation accélération + vitesse + position qui nous serviront par la suite. La difficulté réside à présent dans le calcul des forces afin de déterminer l’accélération.

Simulation de fluides : partie 1

Utilisation d’un kernel

On va employer une fonction de kernel appelée W. Cette fonction possède plusieurs propriétés :

- elle vaut 0 au delà d’un rayon h

- son intégrale vaut 1

- elle a une allure en cloche, est lisse et ses “dérivées” sont lisses

- elle ne dépend que de la distance entre deux points

On utilise cette fonction pour passer de la description “discrète” du milieu (seulement défini sur quelques points) à une description permettant d’obtenir une valeur dans n’importe quel point du plan. On utilise cette fonction est utilisée pour faire une moyenne des valeurs des particules voisines. Avoir une fonction lisse permet d’obtenir un résultat lisse également, avec des variations lisses.

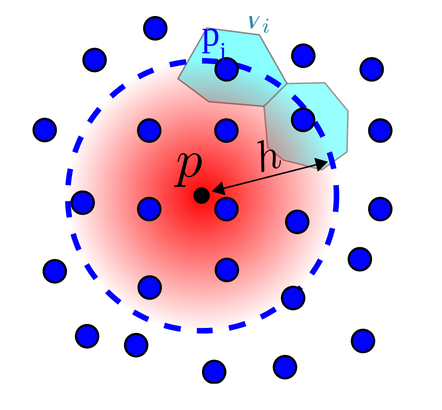
Ici, pour calculer la valeur au point p, on fait la moyenne des valeurs aux particules à une distance ≤h de p. La valeur du kernel est indiquée en rouge: les particules les plus proches vont avoir le plus d’influence sur la valeur totale en p.

On veut également faire contribuer les particules selon leur volume: les particules avec le plus de volume vont contribuer le plus.

Ainsi, on obtient une formule pour obtenir en un point p quelconque la valeur d’une grandeur physique quelconque A :

      A(p)=∑jA(pj)W(||p−pj||)Vj

Avec:

- Aj la valeur de la grandeur physique A associée à la particule j, que l’on suppose connue

- Vj le volume occupé par la particule j

- ||p−pj|| la distance entre le point p et la particule pj

Plutôt que de manipulé Vj, on passe par la masse et la masse volumique ρj :

  Vj=mjρj

Ici, on suppose que chaque particule à la même masse m qui ne varie pas au cours du temps. La formule devient :

  A(p)=∑jA(pj)mρjW(||p−pj||)

Pour appliquer cette formule, on a besoin de connaître la masse volumique ρj de chaque particule. Pour cela, il suffit d’employet la formule! La grandeur physique A devient ρ, ce qui nous donne :

  ρ(p)=∑jρjmρjW(||p−pj||)

  ρ(p)=∑jmW(||p−pj||)

Cette formule, bien qu’apparemment ayant besoin de connaître ρ, n’en a pas besoin ici: on peut donc l’utiliser pour calculer ρ.

Au début de chaque boucle, on actualisera la valeur de ρ pour chaque particule.

Calcul du kernel

Le kernel est une fonction qui “mange” une distance d, et doit avoir les propriétés définies précédemment. Il y a plusieurs choix de fonctions, nous n’irons pas dans les détails de chacune.

On définit d’abord une distance h correspondant au rayon de notre kernel: ici, on peut essayer h=0.02.

On peut ensuite calculer q=d/h : q sera égal à 1 pour d=h (rappel: d correspond à une distance).

On utilise ensuite le cubic spline kernel :

  W(q)=σ(1−1.5q2+0.75q3) pour 0≤q≤1=σ4(2−q)3 pour 1≤q≤2=0 sinon

La constante σ dépend de la dimension: ici, en dimension 2, on a σ=107πh2

On va également avoir besoin de la dérivée W′ :

  W′(q)=σ(−3q+2.25q2) pour 0≤q≤1=−0.75σ(2−q)2 pour 1≤q≤2=0 sinon