Instant Insanity

Définition :

• Instant Insanity est le nom donné par Parker Brothers à leur version de 1967 d'un puzzle qui existe depuis l'Antiquité.

Ce problème se présente de la façon suivante :

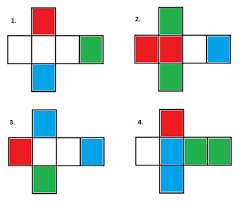
• Vous avez 4 cubes disposez devant vous et sur chacun d'eux se trouve 4 couleurs (autant de couleurs que de cubes).
  • Dans la version de Parker Brother les couleurs était disposée sur les cubes de façon précise.

Dans notre cas il sera possible d'avoir un cubes entièrement d'une couleur ou alors un cube composé de chaque couleurs.

Les REGLES

Il faut aligner les 4 cubes de façon à ce que sans bouger les cubes, les faces de devant, derrière, en haut et en bas contiennent exactement une fois chaque couleurs.

Le Problème

Chaque cube contient 6 faces et si on fixe la face de devant face à nous on peut encore orienter le cube de quatre façon en le faisant pivoter. Comme on peut choisir n'importe qu'elle des 6 faces de chaque cube pour être devant et qu'on peut ensuite la faire pivoter de quatre façon pour choisir les face du haut/bas on arrive à 24 agencement diffèrent par cube. Cela ne parait pas comme ça mais avec nos 4 cubes nous sommes déjà rendu à 331 000 combinaison possible. (Il peut évidement avoir plusieurs combinaisons gagnantes).

• Pour 5 cubes il y a donc 7,9 millions de combinaisons possibles.(Dans le cas ou on rajouterais autant de couleurs que de cube)
• Pour 10 cubes on passe à 69 miles milliards de combinaison.

On retrouve rapidement confronté à un problème, la difficulté à savoir résoudre ce simple puzzle.

Le programme informatique

Quand on voit le nombre grandissant de combinaisons on a envie de crée un un programme informatique afin de toutes les essayer et de nous renvoyer uniquement les agencement de cube qui serait gagnant.