Modélisation de la ruine du joueur

Modélisation de la ruine du joueur

Nous nous intéressons à l'étude des gains d'un joueur lors d'une soirée au casino, dans lequel le joueur joue à la roulette russe.

Le joueur commence avec une somme initiale comprise entre 0 et la somme souhaitée, le joueur s'arrête uniquement si :

  - il obtient la somme souhaitée 
  - le joueur est ruiné (la somme est égale à 0)

Pour cela le joueur va jouer à la roulette en misant à chaque fois 1 jeton qu'il peut doubler ou perdre.

Estimations numériques

Nous allons prendre pour base le document suivant : Ruine

Notre objectif est de trouver de :

- calculer la probabilité de victoire, soit d'atteindre la somme souhaitée, en partant de la somme de départ.
- calculer la durée de la partie, soit le joueur arrête de jouer, donc il atteint l'une des conditions d'arrêt.

On définit de manière générale p la probabilité de victoire d'une partie et q = (1-p)

Estimation de la probabilité de gagner

On veut trouver une formule qui permet de trouver la probabilité de victoire lors d'une soirée au casino selon les paramètres de départ, soit la somme de départ et la somme voulue et la probabilité de victoire.

On commence avec la loi de probabilité totale :

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle P_k(A) = P_k(A|Y_1 = 1)P_k(Y_1 = 1) + P_k(A|Y_1 = -1)P_k(Y_1 = -1) = P_{k+1}(A)p + P_{k-1}(A)q }

Ce qui donne le système suivant :

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \begin{cases} p_k = p \cdot p_{k+1} + q \cdot p_{k-1}, & \text{pour } 1 \leq k \leq a + b \\ p_0 = 0, \\ p_{a+b} = 1. \end{cases} }

On cherche l'équation quadratique :

On a la suite récurrente d'ordre 2 : Résoudre une équation linéaire d'ordre 2
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle p_k = p \cdot p_{k+1} + q \cdot p_{k-1} }

On remplace Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle p_k } par Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle x^{k} }  :
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle x^{k} = p \cdot x^{k+1} + q \cdot x^{k-1} }

On divise par Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle x^{k-1} }  :
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle x = p \cdot x^{2} + q }

On résoult l'équation

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle p \cdot x^{k+1} - x^{k} + q \cdot x^{k-1} = 0 }

Pour p = 1/2

Ca qui donne la solution unique : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle x = 1 }

On en déduit les valeurs Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \alpha \text{ et } \beta }  : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \begin{cases} 0 = \alpha \\ 1 = \alpha + \beta \cdot (a+b) \\ \end{cases} \iff \begin{cases} \alpha = 0 \\ \beta = \frac{a}{a+b} \\ \end{cases} }

On a donc formule suivante : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle p = \frac{a}{a+b} }

Pour p ≠ 1/2

Ce qui donne les solutions : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle x_1 = 1 \text{ et } x_2 = \frac{q}{p} }

On a alors :

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle p_k = \alpha \cdot x_1^{k} + \beta \cdot x_2^{k} }
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \iff p_k = \alpha + \beta \cdot (\frac{q}{p})^{k} }

On en déduit les valeurs Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \alpha \text{ et } \beta }  : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \begin{cases} 0 = \alpha + \beta \\ 1 = \alpha + \beta \cdot (\frac{q}{p})^{k} \\ \end{cases} \iff \begin{cases} \alpha = - \beta \\ 1 = - \beta + \beta \cdot (\frac{q}{p})^{k} \\ \end{cases} \iff \begin{cases} \alpha = - \beta \\ 1 = \beta \left(-1 + \left( \frac{q}{p} \right)^{a+b} \right) \\ \end{cases} \iff \begin{cases} \alpha = - \beta \\ \beta = \frac{1}{-1 + \left( \frac{q}{p} \right)^{a+b}} \\ \end{cases} }

On obtient : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \alpha = -\left(\frac{1}{-1 + \left( \frac{q}{p} \right)^{a+b}}\right) \text{ et } \beta = \frac{1}{-1 + \left( \frac{q}{p} \right)^{a+b}} }

D'où : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle p_a = -\left(\frac{1}{-1 + \left( \frac{q}{p} \right)^{a+b}}\right) + \frac{\left( \frac{q}{p} \right)^{a}}{-1 + \left( \frac{q}{p} \right)^{a+b}} \iff p = \frac{\left( \frac{q}{p} \right)^{a} - 1}{\left( \frac{q}{p} \right)^{a+b} - 1} }

On a donc formule suivante : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle p = \frac{\left( \frac{q}{p} \right)^{a} - 1}{\left( \frac{q}{p} \right)^{a+b} - 1} }

Estimation du temps moyen de jeu

On commence avec la loi de probabilité totale :

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle E_k(T) =E_k(T|Y_1 = 1)P(Y_1 = 1) + E_k(A|Y_1 = -1)P(Y_1 = -1) = (1 + E_{k+1}(T))p + (1 + E_{k-1}(T))q }

Ce qui donne l'équation :

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \begin{cases} e_k = 1 + p \cdot e_{k+1} + q \cdot e_{k-1}, & \text{pour } 1 \leq k \leq a + b \\ e_0 = 0, \\ e_{a+b} = 0. \end{cases} }

On note, pour Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle k \geq 1 , d_k = e_k - e_{k-1} }

On a donc la relation de récurence : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle 0 = 1 + p \cdot d_{k+1} - q \cdot d_k }

Pour p = 1/2

On a Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \frac{1}{2} \cdot d_{k+1} = \frac{1}{2} \cdot d_{k} - 1 }

donc, Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle d_{k+1} = d_k - 2 }

d'où Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle d_k = d_1 - 2 \left(k-1 \right) }

Alors pour Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle n \geq 1 , e_n = \sum_{k=1}^{n} d_k = n \cdot d_1 - 2 \cdot \sum_{k=0}^{n-1}k = n \cdot d_1 - 2 \cdot \frac{n(n-1)}{2} = n(d_1 - (n - 1)) }

Or Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle e_{a+b} = 0 = (a+b)(d_1 + (a + b - 1)), \text{d'où } d_1 = a + b - 1 }

Donc Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle E[T] = e_a = a(a + b - 1 - (a - 1)) = ab }

Pour p ≠ 1/2

On pose le réel l qui verifie Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle 0 = pl - ql } qui est donc Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle l = \frac{1}{q-p} }

La relation devient donc Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle 0 = p(d_{k+1} - l) - q(d_k - l) }

Par conséquent, Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle d_{k+1} - l = \frac{q}{p}(d_k - l) , \text{et donc } d_k - l = \left( \frac{q}{p} \right) ^{k-1} (d_1 - l) }

Donc pour Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle n \geq 1 } , on a :

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle e_n = \sum_{k=1}^{n}d_k + e_0 = \sum_{k=1}^{n} \left( l + \left( \frac{q}{p} \right) ^{k-1} \cdot (d_1 - l) \right) = nl + (d_1 - l) \cdot \sum_{k=0}^{n-1}\left( \frac{q}{p} \right) ^{k} = nl + (d_1 - l) \cdot \frac{1 - \left( \frac{q}{p} \right) ^{n}}{1 - \frac{q}{p}}}

Or Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle e_{a+b} = 0 = (a+b)l + (d_1 - l) \cdot \frac{1 - \left( \frac{q}{p} \right) ^{a+b}}{1 - \frac{q}{p}} \text{par conséquent :} \frac{d_1 - l}{1 - \frac{q}{p}} = -\frac{(a+b)l}{1 - \left( \frac{q}{p} \right) ^{a+b} }}

Donc Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle E[T] = e_a = al - \left( 1 - \left( \frac{q}{p} \right)^{a} \right) \cdot \frac{(a+b)l}{1 - \left( \frac{q}{p} \right) ^{a+b}} = \frac{1}{q-p} \cdot \left( a - (a+b) \cdot \frac{1 - \left( \frac{q}{p} \right) ^{a} }{1 - \left( \frac{q}{p} \right) ^{a+b} } \right) = \frac{(a+b)p-a}{p-q} }

Simulation d'une partie

Afin de modéliser la ruine du joueur on peut utiliser ce programme python :

Bases du Programme

On commence par initialiser nos valeurs que l'on va utiliser :

from random import random
from matplotlib import pyplot as plt 

PROBABILITE = (18/37) #18/37 Pour la roulette
SOMME_DEPART = 10
GAIN_FIN = 10  # Le gain souhaité

#Faire varier Nombre de Parties 

NOMBRE_PARTIES = 1000

Simulation d'une soirée

On commence par simuler une soirée au casino :

def simule_soiree(initial:int = SOMME_DEPART, fin:int= GAIN_FIN, prob:int= PROBABILITE) -> tuple:
    """ Simule une soirée au casino """
    
    tab = [initial]
    somme = initial 
    
    while somme > 0 and somme < initial + fin:
        aleatoire = random()
        if aleatoire <= prob:
            somme += 1
        else:
            somme -= 1
        tab = tab + [somme]
        
    if somme == initial + fin:
        res = True
    else:
        res = False
        
    return (tab, res)

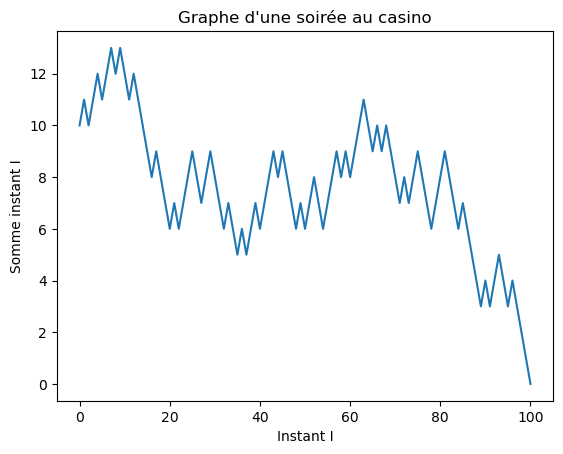
On peut afficher le résultat d'une soirée :

 
# Permet d'afficher une partie jouée.

def affiche_graphe() -> None:
    """ Affiche le graphe d'une soirée au casino """

    y = simule_soiree()[0]
    x = [[i] for i in range(len(y))]
    plt.title("Graphe d'une soirée au casino") 
    plt.xlabel("Instant I") 
    plt.ylabel("Somme instant I") 
    plt.plot(x,y) 
    plt.show()
    
affiche_graphe()

Verifications de nos estimations numériques

Pour cette partie nous commençons à 10 jetons et on veut doubler cette somme.

On peut implémenter nos estimations numériques :

 
R = (1-PROBABILITE) / (PROBABILITE)

def calcule_proba_victoire_theorique() -> float:
    """Renvoie la probabilité de victoire théorique"""
    
    if PROBABILITE == 0.5:
        res = (SOMME_DEPART) / (SOMME_DEPART + GAIN_FIN)
        
    else:
        numerateur = R**(SOMME_DEPART) - 1
        denumerateur = (R**(SOMME_DEPART + GAIN_FIN) - 1)
        res = numerateur / denumerateur
    
    return res

def calcule_duree_partie_theorique() -> float:
    """Renvoie la durée theorique d'une partie"""
    
    if PROBABILITE == 0.5:
        res = SOMME_DEPART * GAIN_FIN
        
    else:
        numerateur = (SOMME_DEPART + GAIN_FIN) * (1 - R**SOMME_DEPART)
        denumerateur = 1 - R**(SOMME_DEPART + GAIN_FIN)
        
        res = (1 / (2 * PROBABILITE - 1)) * ((numerateur / denumerateur) - SOMME_DEPART)
    
    return res

On va utiliser la méthode de comptage pour observer nos simulations :

def calcule_nombre_victoire(tab_parties = SIMULATION_N_SOIREE) -> int:
    """ Renvoie le nombre de victoires dans les soirées simulées"""
    compteur = 0
    
    for res_partie in tab_parties:
        if res_partie[1] == True:
            compteur = compteur + 1
    
    return compteur

def calcule_proba_victoire(tab_parties = SIMULATION_N_SOIREE) -> float:
    """Renvoie la probabilité de victoire sur M soirées"""
    
    nb_victoires = calcule_nombre_victoire(tab_parties)
    res = nb_victoires/len(tab_parties)
    
    return res


def calcule_duree_moyenne():
    """ Renvoie la durée moyenne sur M soirées simulées"""
    somme = 0
    for partie in SIMULATION_N_SOIREE:
        duree_partie = len(partie[0])
        somme += duree_partie
    res = somme / NOMBRE_PARTIES
    return res

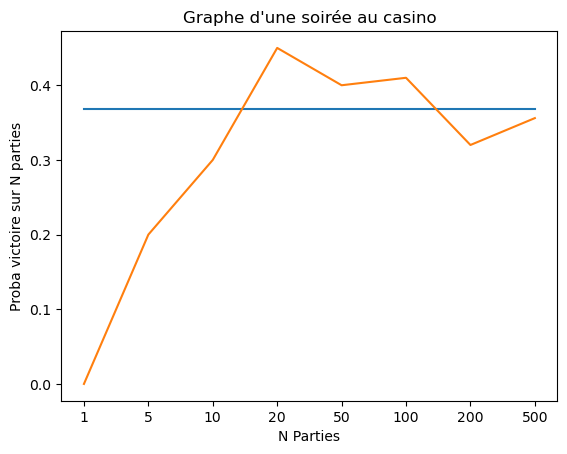
On peut maintenant comparer nos résultats :

 
Voici les valeurs theoriques : 

   La probabilité de victoire : 0.3680312223171822
   Durée partie moyenne theorique : 97.65689548528538

Voici les valeurs avec nos resultats : 

   La probabilité de victoire : 0.347
   Durée partie moyenne : 95.984

Nous pouvons ainsi voir que nos formules qui servent à estimer la probabilité de victoire sont assez bonnes.

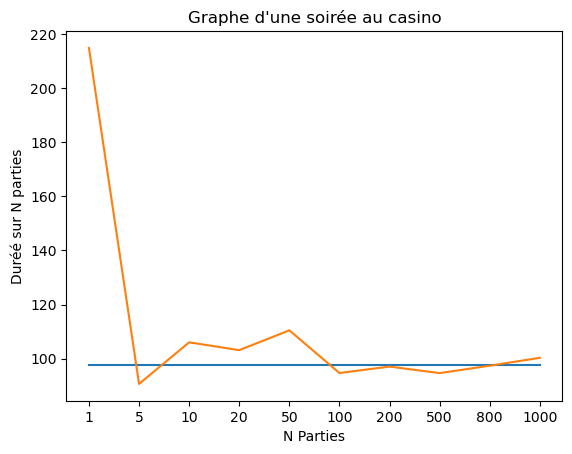
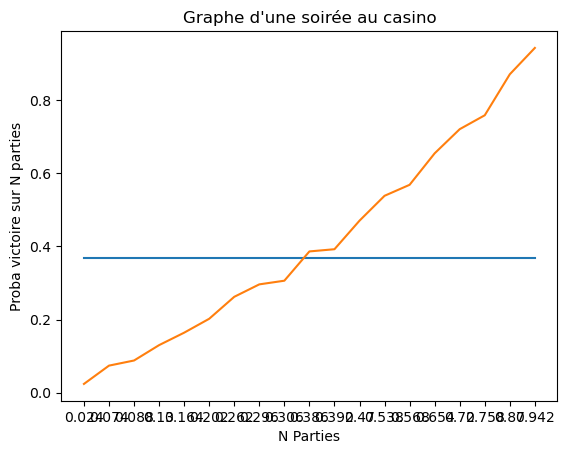
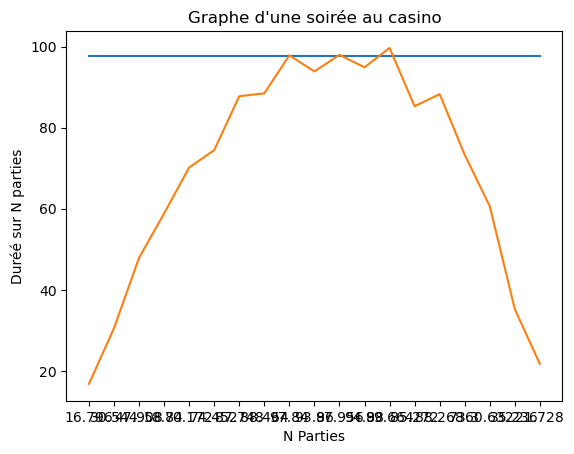
Nous pouvons dresser un graphe de l'évolution de la probabilité de victoire et la durée selon le nombre de parties simulées.

En bleu, nous avons la probabilité de victoire théorique.

En bleu, nous avons la durée théorique.

Autres Graphes

Nous pouvons aussi faire des graphes pour modeliser l'évolution de la probabilité et de la durée selon la somme de départ.

Dans notre cas nous allons faire varier la somme de départ de 1 à 19. La somme souhaité est donc 20.

Nous avons ci-dessous le graphe de l'évolution de la probabilité de victoire.

Nous avons ci-dessous le graphe de l'évolution de la durée.