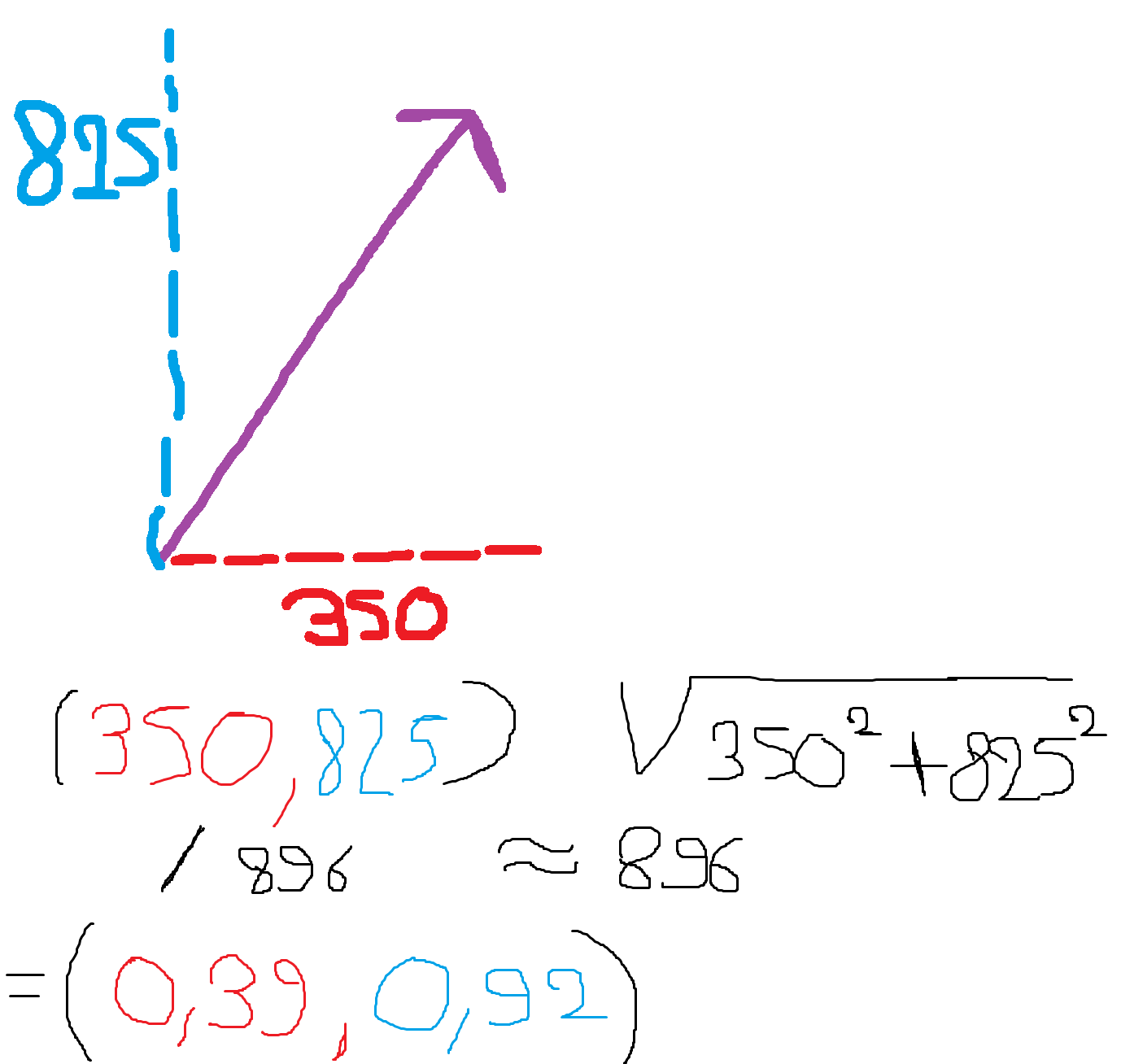« Magic Numbers et Jeux Vidéo » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| Ligne 51 : | Ligne 51 : | ||
Si je vous demande de calculer la racine carré de 2531 de tête vous n'y arriverai certainement pas. Pour notre pc c'est pareil, il ne sort pas ce résultat par magie. |
Si je vous demande de calculer la racine carré de 2531 de tête vous n'y arriverai certainement pas. Pour notre pc c'est pareil, il ne sort pas ce résultat par magie. |
||
Il existe une multitudes d'algorithmes permettant de trouver cela, nous allons nous intéresser à deux de ces algorithmes. |
|||
Pour sortir ce résultat, il utilise l'algorithme de Newton-Raphson qui permet de calculer la racine carré d'un nombre. |
|||
(En vrai dans les nouveaux processeurs les calculs de racine sont mieux optimisés aujourd'hui) |
|||
Intéressons nous à cet algorithme. |
|||
<h1 style="font-family:Impact, Haettenschweiler, 'Arial Narrow', sans-serif">Méthode pour calculer des racines carrés</h1> |
<h1 style="font-family:Impact, Haettenschweiler, 'Arial Narrow', sans-serif">Méthode pour calculer des racines carrés</h1> |
||
Dans cette partie, nous allons |
Dans cette partie, nous allons nous intéresser à deux algorithmes : |
||
- Celui de Newton-Raphson |
- Celui de Newton-Raphson |
||
| Ligne 68 : | Ligne 65 : | ||
<h2 style="font-family:Impact, Haettenschweiler, 'Arial Narrow Bold', sans-serif">Méthode Newton-Raphson</h2> |
<h2 style="font-family:Impact, Haettenschweiler, 'Arial Narrow Bold', sans-serif">Méthode Newton-Raphson</h2> |
||
La méthode de Newton Raphson est une méthode itérative qui permet de trouver une approximation d'une racine. |
|||
Cela signifie que la précision de notre résultat dépend uniquement du nombre d'itération appliqué à notre nombre initial. |
|||
Avec <math>x</math>, le nombre dont on cherche la racine, voici à quoi ressemble la suite nous permettant d'obtenir la racine carré d'un nombre : |
|||
<math> |
|||
y_{n+1} = \frac{1}{2} \left( y_n + \frac{x}{y_n} \right) |
|||
</math> |
|||
Donc par exemple pour trouver la racine de 25 on peut réaliser cette application numérique : |
|||
<math> |
|||
y_0 = 1 \quad \text{(valeur initiale)} |
|||
</math> |
|||
<math> |
|||
y_1 = \frac{1}{2} \left( y_0 + \frac{25}{y_0} \right) = \frac{1}{2} \left( 1 + \frac{25}{1} \right) = \frac{1}{2} \times 26 = 13 |
|||
</math> |
|||
<math> |
|||
y_2 = \frac{1}{2} \left( y_1 + \frac{25}{y_1} \right) = \frac{1}{2} \left( 13 + \frac{25}{13} \right) = \frac{1}{2} \times 14.923 \approx 7.4615 |
|||
</math> |
|||
<math> |
|||
y_3 = \frac{1}{2} \left( y_2 + \frac{25}{y_2} \right) = \frac{1}{2} \left( 7.4615 + \frac{25}{7.4615} \right) = \frac{1}{2} \times 9.985 = 4.9925 |
|||
</math> |
|||
<math> |
|||
y_4 = \frac{1}{2} \left( y_3 + \frac{25}{y_3} \right) = \frac{1}{2} \left( 4.9925 + \frac{25}{4.9925} \right) = \frac{1}{2} \times 5.0001 \approx 5.0000 |
|||
</math> |
|||
Comme nous pouvons le voir, cette méthode donne une approximation plutôt pas mal. |
|||
Mais cette méthode pose un problème. Pour avoir une bonne approximation, il faut réaliser plusieurs itération donc c'est une opération longue. |
|||
Certes cette méthode est considéré comme à 'convergence quadratique', ce qui signifie qu'on obtient un nombre cohérent en très peu d'itération. |
|||
Mais encore faut il donner un nombre d'itération au préalable. Et nous ne connaissons pas ce nombre. |
|||
Mais ces défaut majeurs ont une solution, cette solution est la prochaine méthode que nous allons voir. |
|||
<h2 style="font-family:Impact, Haettenschweiler, 'Arial Narrow Bold', sans-serif">Méthode des carré inverse rapide</h2> |
|||
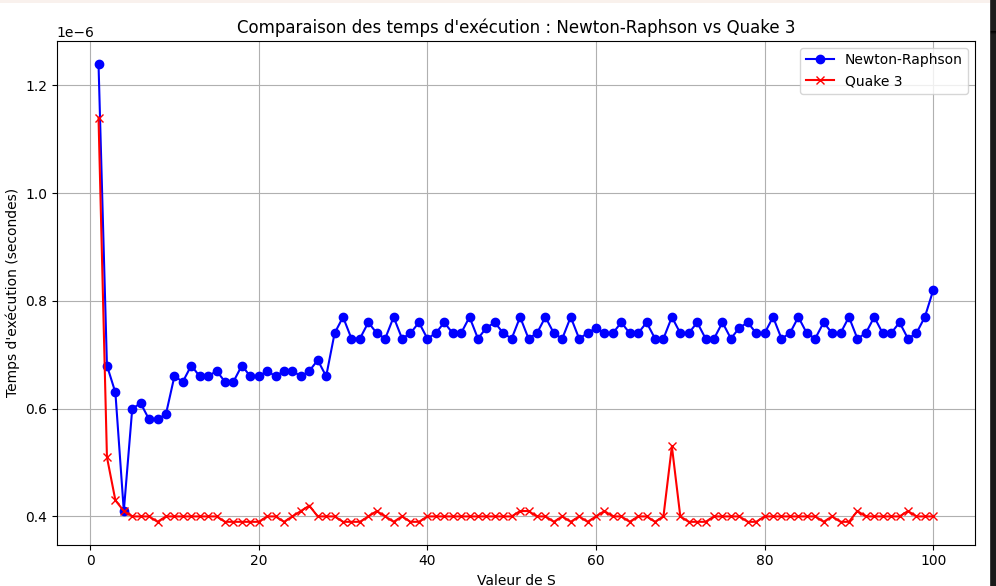
<h2 style="font-family:Impact, Haettenschweiler, 'Arial Narrow Bold', sans-serif">Quel méthode est la meilleure ?</h2> |
|||
[[Fichier:Noah_cuneo_newtonvsquake3.png|none|400px|thumb|Perception - jeu réalisé en VISI301]] |
[[Fichier:Noah_cuneo_newtonvsquake3.png|none|400px|thumb|Perception - jeu réalisé en VISI301]] |
||
Version du 9 mars 2025 à 18:52
Noah CUNEO
Tuteur : François BOUSSION
Introduction
Les Magic Numbers, c'est mal !
Mais nous allons voir que dans certains cas de figure... C'est plutôt ok.
Dans un premier temps, rappelons nous ce qu'est un magic number.
Nous sommes tenté de dire qu'un magic number est une constante. Et bien c'est partiellement vrai...
En réalité, une constante et une valeur nommée et explicite. Comme par exemple PI (3.1415...) ou la constante gravitationelle G (9.81).
Alors qu'un magic number est une valeur qui semble sortir de nulle part, par exemple 0x5f3759df.
Vous devez vous dire que cette valeur que j'ai donné, je la sort de nulle part. Et bien non ! Cette valeur est extrêmement utile dans bien des domaine.
D'abord faisons quelques rappels.
Normaliser un vecteur
La normalisation de vecteur est une notion importante des mathématiques et de l'informatique.
Par exemple, pour le jeu que nous avons réalisé en VISI301, nous avons dû normaliser le vecteur existante entre le centre de l'écran et la souris.
Ce dernier permettant de gérer la trajectoire d'un projectile.
Pourquoi le normaliser ? Et bien parce que si nous utilisons le vecteur dont je viens de vous parler, la balle irai plus ou moins vite en fonction de la distance entre la souris et le centre de l'écran.
Voici un rappel de comment nous pouvons normaliser un vecteur :
Nous avons maintenant un vecteur normalisé. Ainsi, notre balle aura une vitesse constante peut importe la distance de la souris.
Et nous pouvons par ailleurs multiplier notre vecteur par un scalaire pour avoir un contrôle total sur la vitesse du projectile.
On a normalisé un vecteur, c'est bien... Mais n'est ce pas un peu lent comme méthode de calcul ?
Si je vous demande de calculer la racine carré de 2531 de tête vous n'y arriverai certainement pas. Pour notre pc c'est pareil, il ne sort pas ce résultat par magie.
Il existe une multitudes d'algorithmes permettant de trouver cela, nous allons nous intéresser à deux de ces algorithmes.
Méthode pour calculer des racines carrés
Dans cette partie, nous allons nous intéresser à deux algorithmes :
- Celui de Newton-Raphson
- Celui de la racine carré inverse rapide
Méthode Newton-Raphson
La méthode de Newton Raphson est une méthode itérative qui permet de trouver une approximation d'une racine.
Cela signifie que la précision de notre résultat dépend uniquement du nombre d'itération appliqué à notre nombre initial.
Avec Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle x} , le nombre dont on cherche la racine, voici à quoi ressemble la suite nous permettant d'obtenir la racine carré d'un nombre :
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle y_{n+1} = \frac{1}{2} \left( y_n + \frac{x}{y_n} \right) }
Donc par exemple pour trouver la racine de 25 on peut réaliser cette application numérique :
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle y_0 = 1 \quad \text{(valeur initiale)} }
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle y_1 = \frac{1}{2} \left( y_0 + \frac{25}{y_0} \right) = \frac{1}{2} \left( 1 + \frac{25}{1} \right) = \frac{1}{2} \times 26 = 13 }
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle y_2 = \frac{1}{2} \left( y_1 + \frac{25}{y_1} \right) = \frac{1}{2} \left( 13 + \frac{25}{13} \right) = \frac{1}{2} \times 14.923 \approx 7.4615 }
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle y_3 = \frac{1}{2} \left( y_2 + \frac{25}{y_2} \right) = \frac{1}{2} \left( 7.4615 + \frac{25}{7.4615} \right) = \frac{1}{2} \times 9.985 = 4.9925 }
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle y_4 = \frac{1}{2} \left( y_3 + \frac{25}{y_3} \right) = \frac{1}{2} \left( 4.9925 + \frac{25}{4.9925} \right) = \frac{1}{2} \times 5.0001 \approx 5.0000 }
Comme nous pouvons le voir, cette méthode donne une approximation plutôt pas mal.
Mais cette méthode pose un problème. Pour avoir une bonne approximation, il faut réaliser plusieurs itération donc c'est une opération longue.
Certes cette méthode est considéré comme à 'convergence quadratique', ce qui signifie qu'on obtient un nombre cohérent en très peu d'itération.
Mais encore faut il donner un nombre d'itération au préalable. Et nous ne connaissons pas ce nombre.
Mais ces défaut majeurs ont une solution, cette solution est la prochaine méthode que nous allons voir.
Méthode des carré inverse rapide