Introduction à la complexité et sa formalisation

Étudiant : ALBRECHT Maël

Tuteur : HIRSCHOWITZ Tom

Introduction

Pour introduire notre sujet nous allons partir d'un exemple, imaginer que vous vouliez trier des fichiers dans votre ordinateur ( dans notre cas des fichiers numéroter et par exemple nous souhaitons les triés par ordre croissant). Pour effectuer cette tache vous pouvez donc créer un programme qui le ferra pour vous. Malheureusement, votre programme prend beaucoup de temps a s'exécuter. Pour résoudre ce problème on se tourne vers la complexité.

Complexité

La complexité permet de mesurer l'efficacité des fonctions. Elle dépend de différents critères tel que :

• le temps de calcul séquentiel , c'est a dire le temps qui es mis pour exécuter toute les instructions une par une.

• le temps de calcul parallèle , c'est a dire le temps qui es mis pour exécuter toute les instructions avec plusieurs processeur donc avec des opération exécuté en simultané.

• l'esapace disque nécessaire a ces opération qui peut donc ralonger le temps d'execution d'une opérations.

• ainsi que beaucoup d'autre paramètre...

Pour illustrer cela nous allons utiliser deux fonctions « identité » comme exemple.

On commence donc par définir un type d'entier unaires.

1.   type nat = Z | S of nat
2.   let one = S Z
3.   let two = S (S Z) (* etc.. *)

On programme ensuite une fonction identité simple :

1.   let id1 n = n

Et une fonction identité qui inspecte son argument, puis le reconstruit :

1.   let rec id2 n = match n with
2.   | Z -> Z
3.   | S p -> S (id2 p)

Complexité en temps

On s'intéresse au nombre d'étape de calcul en fonction de la taille de l'argument.

On fait souvent des hypothèses simplificatrices pour calculer une complexité, bien sur celle ci doive être simplificatrice mais rester vrai. Ici nous comptons le nombre de tests match ... with.

• Pour id1 : 0.
• Pour id2 : autant $que$ la taille de l'argument.

Notation O

Nous allons en suite introduire la notation O (dite « grand o »).

Pour cela fixons des types A et B et une « manière de compter ».

On définis donc une fonction f: A -> B.

Cette fonction f nous permet de prendre la taille de a et de trouver le temps avec f(a) soit :

taille(a) -> temps(f(a))

Cela nous permet donc de trouver :

id1: n -> 1 id2: n -> n

Pour présenter cela nous utilisons la notation suivante :

• Complexité de id1 : O(1)
• Complexité de id2 : O(n)

Si l'on souhaite développer cela, nous pouvons prendre :

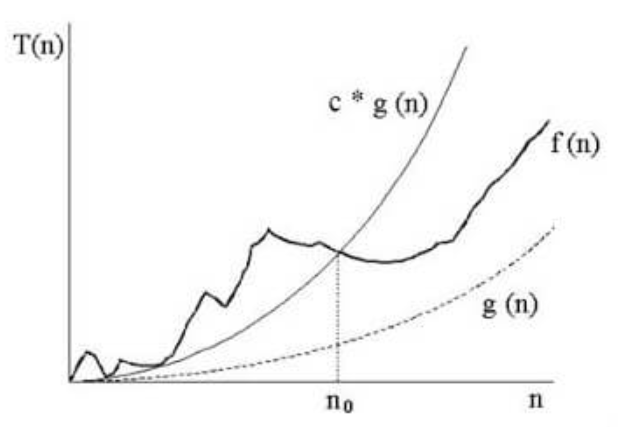
f ∈ O(g) qui signifie f(n) ≤ c * g(n)

Avec :

• c une constante bien choisie
• et pour tout n ≥ n_0

Langages utilisés

Pour créer nos différentes fonctions et comprendre leur complexité nous avons utiliser deux langage différent :

• Le langage OCaml, un langage fonctionnel et fortement typé.

• Le langage Agda, qui est un langage fonctionnel, typé et qui sert en partie programmer des preuves mathématiques.
• On utilise aussi une extension d'Agda qui se nomme Calf et qui sert a calculer la complexité d'une fonction sous forme de coûts.