Introduction à la complexité et sa formalisation

Étudiant : ALBRECHT Maël

Tuteur : HIRSCHOWITZ Tom

Introduction

Pour introduire notre sujet nous allons partir d'un exemple, imaginez que vous vouliez trier des fichiers dans votre ordinateur (dans notre cas des fichiers numérotés et par exemple nous souhaitons les trier par ordre croissant). Pour effectuer cette tâche vous pouvez donc créer un programme qui le fera pour vous. Malheureusement, votre programme prend beaucoup de temps à s'exécuter. Pour résoudre ce problème on se tourne vers la complexité.

Complexité

La complexité permet de mesurer l'efficacité des fonctions. Elle dépend de différents critères tels que :

• Le temps de calcul séquentiel , c'est-à-dire le temps qui est mis pour exécuter toutes les instructions une par une.

• Le temps de calcul parallèle , c'est-à-dire le temps qui est mis pour exécuter toutes les instructions avec plusieurs processeurs donc avec des opérations exécutées simultanément.

• L'espace mémoire nécessaire, qui peut rallonger le temps d'exécution d'une opération.

• Ainsi que d'autres paramètres…

Pour illustrer cela nous allons utiliser deux fonctions « identité » comme exemple.

On commence donc par définir un type d'entier unaire.

1.   type nat = Z | S of nat
2.   let one = S Z
3.   let two = S (S Z) (* etc.. *)

On programme ensuite une fonction identité simple :

1.   let id1 n = n

Et une fonction identité qui inspecte son argument, puis le reconstruit :

1.   let rec id2 n = match n with
2.   | Z -> Z
3.   | S p -> S (id2 p)

Complexité en temps

On s'intéresse au nombre d'étapes de calcul en fonction de la taille de l'argument.

On fait souvent des hypothèses simplificatrices pour calculer une complexité. Toutefois, celles-ci doivent rester vraies. Ici nous comptons le nombre de tests match ... with.

• Pour id1 : 0.
• Pour id2 : autant que la taille de l'argument.

Notation O

Nous allons ensuite introduire la notation O (dite « grand o »).

Pour cela, fixons des types A et B et une « manière de compter ».

On définit donc une fonction f: A -> B.

Cette fonction f nous permet de prendre la taille de a et de trouver le temps avec f(a) soit :

taille(a) -> temps(f(a))

Cela nous permet donc de trouver :

id1: n -> 1

id2: n -> n

Pour présenter cela nous utilisons la notation suivante :

• Complexité de id1 : O(1)
• Complexité de id2 : O(n)

Si l'on souhaite développer cette notation, nous pouvons prendre :

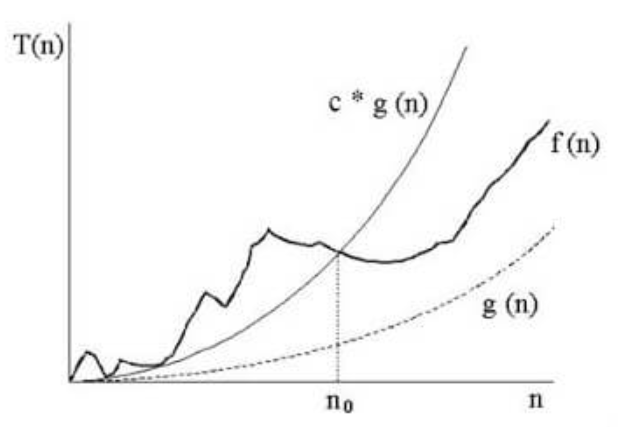
f ∈ O(g),ce qui signifie :f(n) ≤ c * g(n)

Avec :

• c une constante bien choisie
• et pour tout n ≥ n_0

Langages utilisés

Pour créer nos différentes fonctions et comprendre leur complexité nous avons utilisé deux langages différents :

• Le langage OCaml, un langage fonctionnel et fortement typé.

• Le langage Agda, qui est un langage fonctionnel, typé et qui sert en partie à programmer des preuves mathématiques.
• On utilise aussi une extension d'Agda appelée Calf et qui sert à calculer la complexité d'une fonction sous forme de coûts.

Tri en OCaml

Nous allons donc écrire différentes fonctions de tri dans le langage OCaml.

Tri par insertion en OCaml

Tout d'abord, le tri par insertion consiste à :

• Prendre en argument une liste à trier.
• Prendre une liste vide.
• Prendre un élément de la liste non triée.
• Insérer cet élément au bon endroit dans la liste vide (il faut donc parcourir la liste).
• Puis on recommence le processus de sorte à trier cette liste et à renvoyer celle-ci.

Il faut donc avoir en tête que nous manipulons bien deux listes différentes pendant l'exécution.

Pour faire cela en OCaml nous avons besoin de la fonction d'insertion :

1.   let rec insert e l = match l with
2.   [] -> [e]
3.   | x :: l' -> if e <= x
4.     then e :: l
5.     else x :: (insert e l')

Cette fonction est une fonction récursive qui s'appelle donc elle-même. On peut donc voir que si la liste fournie est vide, alors elle renvoie l'élément e, sinon elle insert un élément au bon endroit.

Nous avons ensuite besoin de la fonction de tri :

1.   let rec trie l = match l with
2.   [] -> []
3.   | e::l' -> insert e (trie l')

Cette fonction est aussi une fonction récursive qui va appeler notre fonction d'insertion pour trier la liste fournie en argument.

Pour la complexité de cette fonction nous allons compter le maximum de tests que peut faire trie l. On trouve que pour chaque élément de la liste l' le coût augmente de 1.

On se retrouve donc avec une complexité totale qui correspond à la somme des éléments de 1 à n-1 soit (n(n-1))/2 ce qui représente une complexité O(n²).

Tri par fusion en OCaml

Nous nous intéressons donc maintenant à une fonction de tri par fusion. Le principe de cette fonction est le suivant :

• On part d'une liste à trier.
• On effectue une suite de divisions récursives en deux parties jusqu'à obtenir des listes de taille 1.
• On trie ensuite chaque liste.
• Puis on les fusionne entre elles tout en les triant.

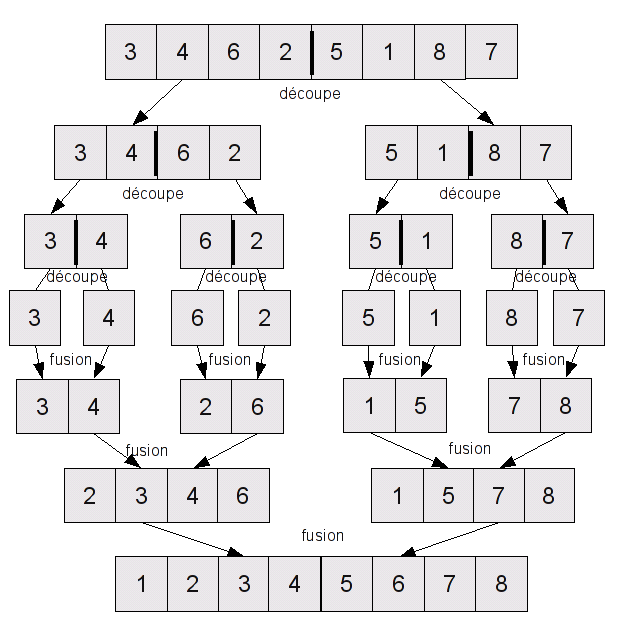
Sur le schéma ci-dessus on peut donc voir une mise en pratique du tri par fusion. On voit la découpe de la liste pour obtenir des listes de tailles 1, puis le tri et la fusions des différentes listes de sorte a créer une liste triée.

Pour faire cela en OCaml, on doit tout d'abord écrire la fonction coupe qui est créée grâce à la fonction coupe_rec :

1.   let rec coupe_rec n jusquici l =
2.   if  n = 0 then List.rev jusquici , l
3.   else coupe_rec (n-1) (List.hd l :: jusquici) (List.tl l)

La fonction coupe_rec est une fonction récursive, elle permet de couper une liste en deux.

1.   let coupe l = coupe_rec (List.length 1 /2) [] l

La fonction coupe utilise donc la fonction coupe_rec. Elle va donc nous permettre de couper la liste en plusieurs listes d'un élément. Il nous faut ensuite écrire la fonction fusionne :

1.   let rec fusionne l1 l2 = match l1 with
2.   | [] -> l2
4.   | e::l1' -> match l2 with
5.       | [] -> l1
6.       | x::l2' -> if e <= x
7.                   then e :: fusionne l2 l1'
8.                   else x :: fusionne l1 l2'

Cette fonction est une fonction récursive, elle compare un élément d'une liste et regarde où l'ajouter pour que cela crée une liste triée à partir de deux listes.

Enfin nous créons la fonction trieFusion :

1.   let rec trieFusion l = match l with
2.   | [] -> []
3.   | [e] -> [l]
4.   | _ -> let l1, l2 = coupe l in
5.       fusionne (triFusion l1) (trieFusion l2)

La fonction trieFusion effectue donc les tâches suivantes : (Cette fonction est une fonction récursive)

• Si on rentre une liste vide, cela renvoie une liste vide,
• Si on rentre une liste à un seul élément, on renvoie la liste de cet élément,
• Sinon on appelle notre fonction coupe et notre fonction fusionne pour trier cette liste.

On va donc maintenant s'intéresser à la complexité du tri fusion :

On peut voir que les testes apparaissent dans la phase de fusion. On symbolise donc cette phase par un arbre dont la profondeur est : log2(n).

Dans notre cas on va s'intéresser a un arbre de longueur 2ᵖ ( n = 2^p).

On va donc prendre plusieurs éléments pour montrer cette complexité.

• La profondeur de l'arbre : 0, 1, …, p-3, p-2, p-1, p
• La longueur de la liste n : n = 2^p, n/2 = 2^(p-1), …, 8 = 2^3, 4 = 2^2, 2 = 2^1, 1 = 2^0
• log2(n) = p, p-1, …, 3, 2, 1, 0

On s'intéresse donc à la phase de fusion. Lors de celle-ci, à chaque ligne, chaque test correspond environ à l'insertion d'un élément. Ainsi, dans le pire des cas, l'ensemble des tests correspond environ à l'ensemble des éléments. On obtient donc n tests par changement de ligne. Donc en tout on obtient O(log2(n)*n) tests.

Complexité en Agda/Calf

Pour étudier la complexité en Calf on se sert des deux fonctions identité que l'on a vu précédemment. La fonction id1 qui renvoie tout simplement son arguments, ainsi que la fonction id2 qui inspecte son argument pour le reconstruire et le renvoyer.

Deux fonctions « identité »

On réécrit donc ces deux fonction en Agda/ Calf :

1.   id : cmp((Πnat𝜆_→F nat)
2.   id n = ret n

On a donc bien la fonction id1 ci-dessus.

1.   id : cmp(Πnat𝜆_→F nat)
2.   id zero = ret 0
3.   id (suc n) =
4.      step (F nat) 1 (
5.        bind (F nat) (id n) 𝜆 n' →
6.          ret (suc n'))

On a maintenant notre fonction id2 qui renvoie 0 si l'élément est 0, ou qui regarde le successeur de n.

Pour la seconde fonction (celle qui correspond à id2) on obtient donc bien une complexité de O(n).

1.   id/asymptotic : given nat measured-via (𝜆n→n) , id∈O(𝜆n→n)

Conclusion

En conclusion, nous avons donc vu que la complexité sert à l'optimisation et à la compréhension de nos fonctions. C'est une notion importante dans les différents langages qu'il est essentiel de bien maîtriser. Elle dépend de nombreux critères, plus ou moins complexes à modéliser et à calculer.