Origami, axiomes de Huzita/Justin et ReferenceFinder

L'origami est un art du pliage de papier pour en faire une sculpture, soit géométrique, par exemple une boîte, soit figurative, comme un animal, une fleur, un personnage, etc... qui fut inventé en Chine au 6ème siècle. Depuis la création des ordinateurs, et de programmes dediés à ceux-ci, comme le programme ReferenceFinder, qui utilise les axiomes de Justin-Huzita-Hatori, le pliage de papier est une science qui a été développée virtuellement. L'origami est une science très puissante qui nous permet de faire des choses impossible avec seulement une règle et un compas. L'approfondissement de la géométrie peut se faire à travers le pliage de papier, grâçe aux nouvelles théories créées par celui-ci

Les machines de nos jours nous facilitent la création d'origamis, à travers de nombreux calculs de droites et de points dans un plan.

Les axiomes de Justin-Huzita-Hatori

Ces axiomes ont été inventées par un groupe de 3 personnes : Jacques Justin, Humaki Huzita et Koshiro Hatori. Ils se sont demandés comment trouver tous les plis possibles et inimaginables sur une feuille de papier, en fonction de droites et de points sur celle-ci.

Les axiomes sont au nombre de 7, les 4 premiers étants plutôt basiques et facilement compréhensibles, jusqu'au dernier axiome consistant à résoudre des équations du 3ème degré pour trouver un pli, grace à plusieurs droites et points, et des opérations de perpendicularité ou de parallélisme entre les uns et les autres.

Les 6 premiers axiomes, trouvés par Humaki Huzita ont constitué le fondement de l'étude des constructions géométriques en origami pendant de nombreuses années. Ceux-ci permettent de résoudre des équations quadratiques, cubiques et quartiques avec des coefficients rationnels, des racines cubiques ou permettre de faire la trisection d'un angle.

Le 7ème axiome, découvert par Jacques Justin et Koshiro Hatori après les autres, ne permet pas la solution d'équations d'ordre supérieur aux six axiomes originaux. Mais il est tout de même bien d'avoir l'ensemble complet de tous les axiomes possibles.

Il se peut que certains axiomes soient beaucoup moins utiles que les autres, les derniers axiomes allants chercher dans la compléxité.

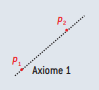
Axiome 1

Étant donnés deux points p1 et p2, il existe un seul pli qui passe par p1 et p2.

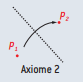
Axiome 2

Étant donnés deux points p1 et p2, il existe un seul pli qui amène p1 sur p2.

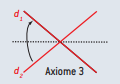
Axiome 3

Étant données deux droites d1 et d2, il existe un seul pli qui amène d1 sur d2.

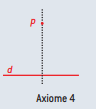
Axiome 4

Étant donnés un point p et une droite d, il existe un pli unique perpendiculaire à d qui passe ce point p.

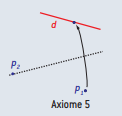
Axiome 5

Étant donnés deux points p1, p2 et une droite d, il existe un seul pli qui place p1 sur d et qui passe par p2.

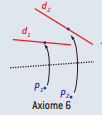
Axiome 6

Étant donnés deux points p1, p2 et deux droites d1, d2, il existe un seul pli qui place p1 sur d1 et place aussi p2 sur d2.

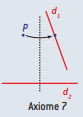
Axiome 7

Étant donnés un point p et deux droites d1, d2, il existe un pli unique qui place p sur d1 et qui est perpendiculaire à d2.

Exemples de l'utilisation des axiomes dans un programme

Les axiomes de Justin-Huzita-Hatori sont fondamentaux pour calculer n'importe quel pli dans un plan. Ainsi, il est possible de créer des programmes qui renvoient des plis dans un plan en fonction de ces axiomes. Nous allons voir les axiomes les plus simples, et le plus compliqué, afin de constater les différences entre eux. La définition d'un point se fait par ses coordonnées x et y, et celle d'un pli peut se faire grace aux coordonnées des 2 points à l'extrémité du plan. Le pli peut aussi se définir par un point et un vecteur directeur du pli, mais cette utilisation ne se fera pas dans les exemples suivants. Les 3 premiers axiomes étants les plus utiles, voici un de leur exemple :

Axiome 1

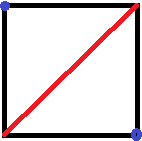
Ici, nous traitons l'axiome le plus simple, qui consiste à simplement lier les 2 points (Dans le cas évident où les 2 points ne sont pas les mêmes).

Point 1 : (0, 0)

Point 2 : (1, 1)

Pli : ((0, 0) , (1, 1))

Axiome 2

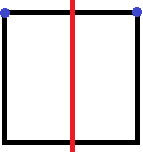
L'axiome 2, qui consiste mathématiquement à calculer la médiatrice du segment (p1,p2) (Dans le cas évident où les 2 points ne sont pas les mêmes), est calculé depuis le milieu du segment et le vecteur normal de celui-ci.

Point 1 : (0, 0)

Point 2 : (0, 1)

Pli : ((0.5, 0) , (0.5, 1))

Point 1 : (0, 0)

Point 2 : (1, 1)

Pli : ((1, 0) , (0, 1))

Axiome 3

Cet axiome peut être considéré comme la bissectrice de l'angle créé par l'intersection des droites d1 et d2. Dans le cas où les 2 droites, et dans le cas où les 2 sont identiques, le pli sera l'une des droites sont parallèles, le pli sera la droite parallèles aux deux autres à égale distance de l'une et de l'autre.