Automates cellulaires
Création en cours.
Ce projet avait pour but d'étudier le fonctionnement des automates cellulaires et les caractéristiques particulières que l'on peut retrouver chez certains.
Définitions
Définition simple
Un automate cellulaire est une grille régulière dont les cases sont appelées « cellules ». Chacune a un « état » parmi un ensemble fini. L'état d'une cellule au « tour » t+1 est définit en fonction de cet état et celui de l'ensemble fini de cellules « voisinage » au tour t, par la « règle » de l'automate cellulaire. Lorsque toutes les cellules ont été mises à jour, on parle de « génération ».
Définition formelle
Un automate cellulaire Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle A} est définit par le 4-uplet Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle (d,Q,V,\delta)} tel que :
- Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle d} est un entier positif, la dimension de Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle A} . Son réseau est donc Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \mathbb{Z}^d}
- Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle Q} est l'ensemble fini des états des cellules de Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle A}
- Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle V \subseteq \mathbb{Z}^d} , un sous-ensemble fini du réseau, le voisinage. Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle V = \{v_1,\ldots,v_a\}}
- Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \delta : Q^a \rightarrow Q} est la règle locale avec Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle a = |V|}
On peut donc définir la fonction globale d'évolution de l'automate Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle F_\delta : Q^{\mathbb{Z}^d} \rightarrow Q^{\mathbb{Z}^d}} définit par Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle F_\delta (c) = z \mapsto \delta\bigl(c(z+v_1),\ldots,c(z+v_a)\bigr)} pour tout Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle c \in Q^{\mathbb{Z}^d}}
Classifications
Bien que les deux classifications qui sont décrites ci-dessous peuvent être retrouvées dans les travaux de certains chercheurs, il est commun de décrire un automate en fonction de leurs caractéristiques particulières sans pour autant les séparer en classes.
Classification de Wolfram
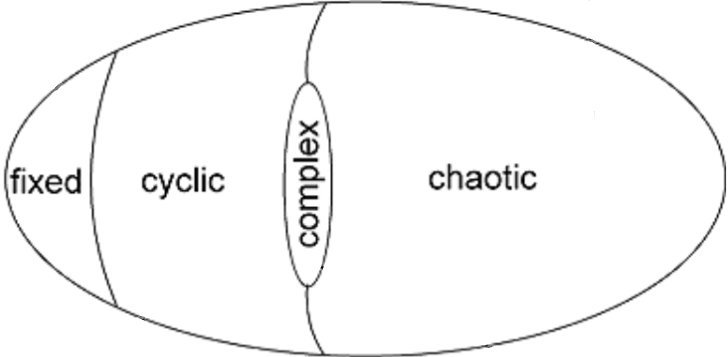
Stephen Wolfram classe les automates cellulaires en 4 classes selon leur comportement avec des configurations initiales aléatoires :
- Stable : Après un certain nombre de générations, une configuration se répète à l'infini.
- Cyclique : Après un certain nombre de générations, une série de configurations se répètent périodiquement.
- Chaotique : Comportement chaotique et génération de motifs apériodiques.
- Complexe : Apparition de structures complexes possédants divers propriétés comme la capacité de se mouvoir ou de se préserver malgré des perturbations.
L'une des principales critiques de cette classification réside dans son incapacité à déterminer si un automate cellulaire est Turin-universel, venant du fait que Wolfram ne définit la classe qu'à partir de configurations initiales aléatoires, mais pas de structure particulière créée spécifiquement. Malgré cela, cette classification reste la plus étudiée.
Christopher Langton propose d'envisager ces classes dans un continuum.
Classification d'Eppstein
Il existe une deuxième classification, proposée par David Eppstein. Les automates sont séparés en 4 classes :
- Expansion obligatoire : N'importe quel motif initial s'étend indéfiniment dans toutes les directions.
- Expansion impossible : Aucun motif ne peut s'étendre au-delà de ses limites initiales.
- Contraction impossible : Les motifs ne s'étendent pas forcément indéfiniment, mais ne peuvent jamais se réduire en-deçà de leur limites initiales.
- Expansion et contraction possibles : Seuls ces cas peuvent contenir des vaisseaux.
À l'heure actuelle, les automates qui ont été prouvés Turing-universels appartiennent tous à la 4ème classe. Cependant il n'a pas été démontré que les autres classes ne peuvent pas contenir d'automate Turing-universel puisqu'il existe d'autres façons de transmettre des informations que les vaisseaux.
Les familles d'automates cellulaires célèbres
Il existe de nombreuses familles d'automates cellulaires, mais nous n'en verrons que deux ici.
Les automates cellulaires élémentaires
Cette famille est la plus simple des automates cellulaires. Ses membres n'ont qu'une dimension et deux états. Le voisinage d'une cellule est composé de celles directement à sa droite et sa gauche et d'elle-même.
Puisque le voisinage prend 3 cellules et que chacune d'elles a un état parmi 2, on a Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle 2^3 = 8} motifs possibles. Pour chaque motif il y a 2 résultats possibles, donc Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle 2^8 = 256} règles possibles pour un automate cellulaire de cette famille. Depuis les travaux de S. Wolfram sur cette famille, chacune de ces règles est nommée par le résultat de ses motifs convertit en décimal.