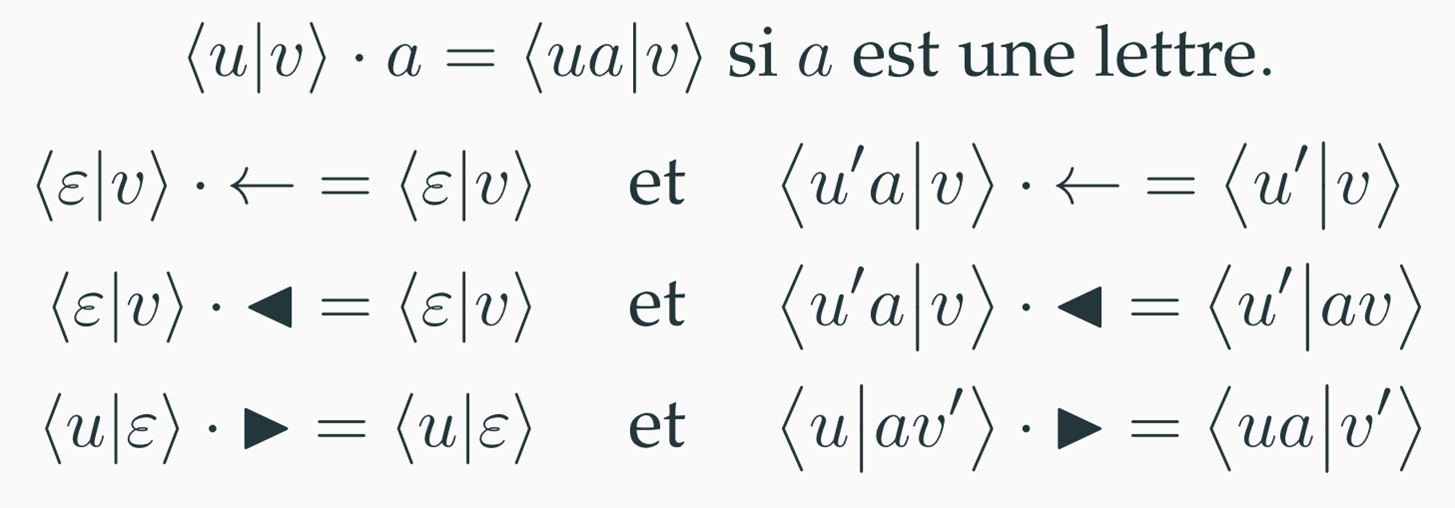Les "claviers"

Chaque touche d'un clavier affiche un caractère. On peut alors écrire tous les mots possibles en appuyant successivement sur les touches pertinentes. Sur un clavier cassé (par exemple, parce qu'il a reçu du café), les touches n'ont plus forcément le comportement attendu : la première touche peut inscrire "ktjh", le seconde "uta", etc. Il n'est alors plus forcément possible d'écrire tous les mots possibles, mais il est facile de comprendre ce que l'on peut faire. Lorsque le comportement de ces touches peut inclure des déplacement (gauche / droite) et la touche "backspace", la situation peut devenir infernale ! Quatre jeunes étudiants en thèse ont récemment développé cette théorie. L'objectif est de se familiariser avec les notions de théorie des langages et de regarder les premiers résultats de cette théorie, les astuces mises en œuvre pour étudier les langages engendrés et les questions ouvertes.

Rappels, définitions et exemples

Rappels :

Un alphabet est un ensemble fini dont les éléments sont des appelés lettres. Exemple : {a,b,c}

Un mot est une suite finie de lettres. Exemple : acabbac est un mot sur l’alphabet {a,b,c}

Un langage est un ensemble de mots. Exemple : a* = {ε, a, aa, aaa, aaa, a…a} sur le clavier {a}

Définitions :

Un clavier est un ensemble fini de suite d’opérations élémentaires appelées des touches.

Il existe plusieurs touches spéciales appelées des opérations élémentaires :

• a : ajoute la lettre si elle appartient à l'alphabet

• ← : efface la lettre à gauche du curseur (backspace)

• ◀ : déplace le curseur à gauche

• ▶ : déplace le curseur à droite

• █ : permet de validé la saisi (entrée)

En effet la touche entrée existe car il existe deux types de claviers, les claviers automatiques et les claviers manuels. Les claviers automatiques n’ont pas de notion de fin de série alors que les claviers manuels oui. Il faut donc utilisé des touches acceptantes qui mène a une fin de série après avoir effectué leur action, on peut voir ces touches comme des touches qui se terminent par le symbole entrée.

Exemples :

Le langage (ab+a)*

Ce langage s’écrit avec le clavier K = {ab, a}

C’est l’ensemble des mots qui s’écrivent avec des a et des b, il y a plus ou autant de a que de b.

Le langage a*b*

Ce langage s’écrit avec le clavier K = {a, b<}

C’est l’ensemble des mots qui ont autant de a et de b que l’on veut et tous les a sont avant les b.

Modélisation :

Une configuration s’écrit < u | v > avec u le préfixe, v le suffixe et | le curseur.

On peut donc avoir ce genre de configurations en fonction de l'opération élémentaire utilisée :

Les classes de claviers

On appelle claviers minimaux les claviers automatiques qui ne contiennent aucun symbole spécial. On note MK l’ensemble de ces claviers. On construit toutes les autres classes de claviers en partant d’un clavier minimal et en ajoutant certaines possibilités de symboles spéciaux. Les noms des classes sont obtenus en rajoutant E pour la touche entrée, R pour la touche de suppression à gauche du curseur, G pour la touche de déplacement à gauche et F pour les touches de déplacement. Ainsi, en fonction des symboles spéciaux autorisés, on obtient ces différentes classes .

Classes de claviers

MK {}	GK {<}	FK {<, >}
EK {$}	GEK {<, $}	FEK {<, >, $}
RK {&}	GRK {<, &}	FRK {<, >, &}
REK {&, $}	GREK {<, &, $}	FREK {<, >, &, $}

Remarque : L’utilisation de la touche de déplacement à droite sans la touche de déplacement à gauche est inutile car le curseur est toujours à droite, il est donc inutile de déplacer le curseur à droite.

Le théorème principal

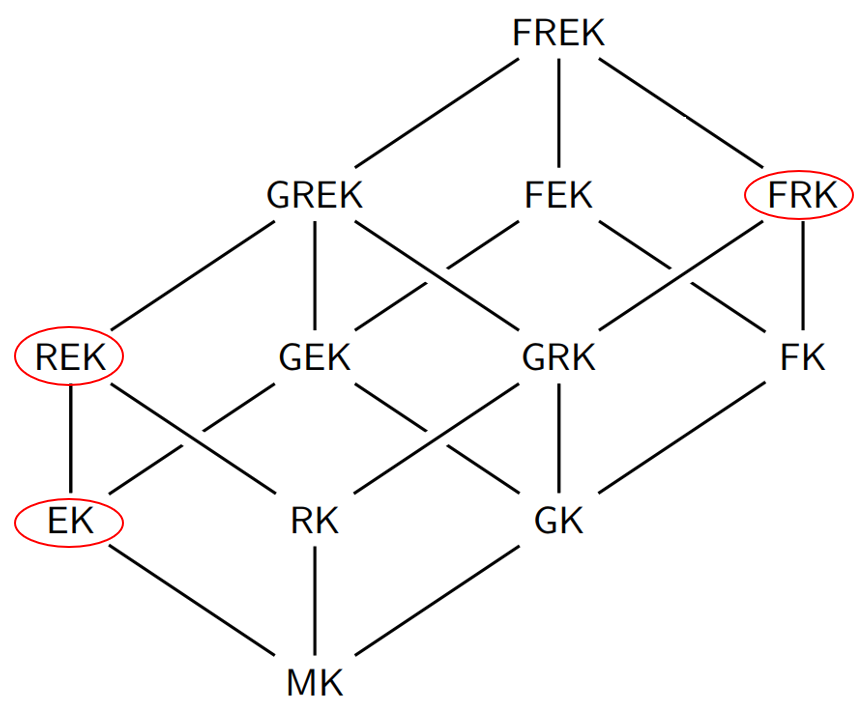
Voici l’ordre exact des classes de claviers :

Les seules inclusions de classes sont les inclusions triviales, sauf peut-être les inclusions de EK et de REK dans FRK.

Ce schéma est un diagramme de Hasse où la relation entre deux éléments est représentée par un segment entre deux points. Si un élément x est inférieur ou égal à un autre élément y, alors le point représentant x est placé plus bas que celui pour y. Ainsi, les segments n'ont pas besoin d'être fléchés pour avoir leur orientation décrite. Lorsque x < y, s'il existe z tel que x < z < y, alors aucun segment ne doit lier x à y.

Théorème (Les claviers sans flèches) :

Pour tous claviers sans flèches, il existe un automate fini reconnaissant le même langage qui est rationnel. Un langage rationnel est un langage qui est décrit par une expression contenant uniquement les lettres et les symboles *, + et . .

Par exemple :

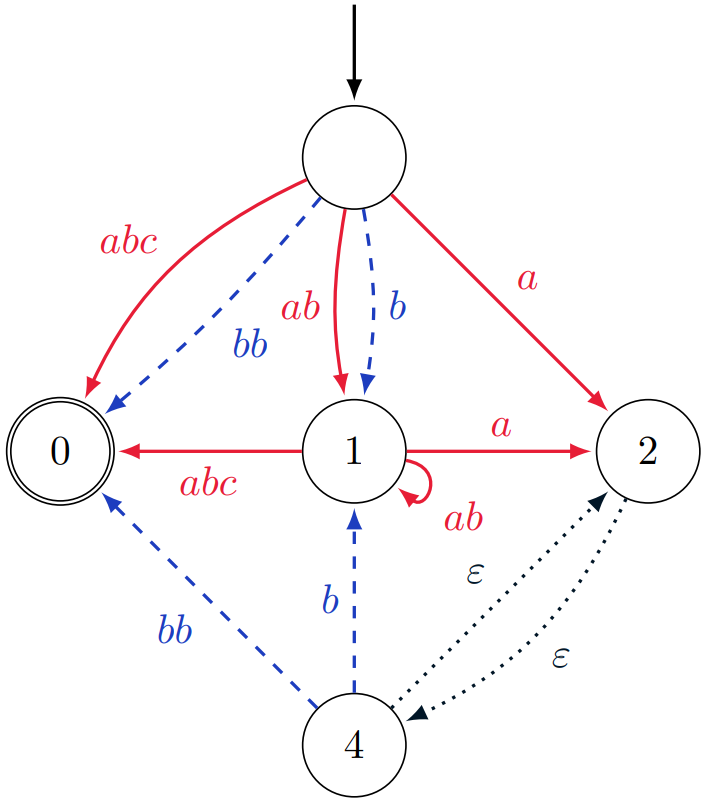
Le clavier K = {←abc, ←←←←bb} reconnait le langage abc + bb + abb + [(ab + b) (ab)* abb] ainsi que le l'automate suivant :

Les transitions en rouge (flèches pleines) correspondent à celles qu’il est possible de faire avec la touche ←abc et les bleues (tirets) à celles qu’on fait avec la touche ←←←←bb. Et finalement, les transitions noires (pointillés), elles, correspondent à utiliser une suite de touches pour passer de i lettres à effacer à j lettres à effacer.

Un langage un peu plus complexe : Le langage a*+b

C’est l’ensemble des mots qui ont autant de a que l’on veut ou qui ne font qu’un b.

On peut se dire que que la création d’un tel clavier n’est pas possible, il faudrait une touche qui fait un certain nombre de a et une touche qui fait un b mais si on utilise les deux touches il y en aura des a avec un b dans le même mot.

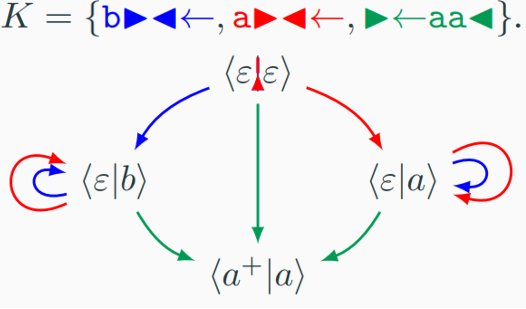
Mais ce langage est possible et il s’écrit avec le clavier K = {b▶◀←, a▶◀←, ▶←aa◀}.

En effet si on regarde l’automate suivant on peut mieux comprendre ce que fait le clavier.

Nommons la touche b▶◀← la touche 1, la touche a▶◀← la touche 2 et la touche ▶←aa◀ la touche 3, On part de la configuration initiale < ε | ε > :

• Si on fait la touche 1, les touches 1 et 2 ne modifient rien par la suite.

• Si on fait la touche 2, les touches 1 et 2 ne modifient rien par la suite.

• Si on fait la touche 3, les touches 1 et 2 ne modifient rien par la suite.

Seulement la touche 3 modifie les configurations précédentes et donne une configuration de la forme < a^n+1 | a > .

Ainsi pour avoir le mot avec un unique b il faut simplement utilisé la touche 1 la première fois et ne pas utilisé la touche 3 le reste.

Annexes (code)