Calibration de caméra et reconstruction 3D

Noah CUNEO

Tuteur : Stéphane BREUILS

Introduction

Nous allons dans ce compte rendu, voir et comprendre ce qu’est la vision par ordinateur.

Plus particulièrement comment à partir d’une caméra nous pouvons traiter l’information d’une image.

Dans le but d’obtenir divers résultats tel que la création d’un panorama ou bien la reconstruction 3D d’un objet à partir de photos.

Pour cela, nous allons nous aider de la bibliothèque OpenCV.

Qui est une bibliothèque conçue spécifiquement pour la vision par ordinateur et le traitement d’images.

*Notons que par soucis de lisibilité, nous allons uniquement afficher des morceaux de code. Mais que nous ferons une redirection systématique vers le code correspondant sur GitHub

Présentation d'OpenCV

OpenCV est donc, comme dit dans l’introduction, une librairie Python axée sur la vision par ordinateur.
En effet, elle propose une grande variété de fonctions utiles au traitement d’images. Comme par exemple :

sift = cv.SIFT_create()
kp = sift.detect(gray,None)

Qui permet de détecter des points clés sur une image.

Ou également par exemple :

M, mask = cv.findHomography(src_pts, dst_pts, cv.RANSAC,5.0)

Qui permet d’estimer une matrice d’homographie.

Mais nous verrons l’utilité de ces fonctions plus en détails ultérieurement.

OpenCV permet également, à l’instar de Tkinter ou Pygame, de générer une interface graphique.

Elle est cependant très limitée puisqu’elle à été créée seulement à l’intention d’afficher des images.

Voici un exemple de comment on affiche une image sur OpenCV :

image = cv2.imread('image.jpg', cv2.IMREAD_GRAYSCALE)
cv2.imshow('Image', image)
cv2.waitKey(0)
cv2.destroyAllWindows()

Ce code va par exemple, afficher l’image « image.jpg » en nuance de gris de cette forme :

Photo d'immeuble en noir et blanc

Nous allons réutiliser cette image ultérieurement, afin que les modifications que nous allons étudier soient mieux compréhensibles.

Présentation de mon code

Lors de ma lecture de la documentation d'OpenCV. J'ai remarqué que certaines tâches pouvaient se répéter.

J'ai donc dans l'optique de rendre mon code plus compréhensible tout en évitant de répéter les tâches déjà effectuées, créé quelque classe permettant d'améliorer ces caractéristiques.

Présentation de mes classes

Voici la classe CameraParametre.

Je l'ai codé afin de stocker dans un fichier dictionnaire les paramètre intrinsèque de la caméra, ainsi que les paramètres extrinsèques pour les images données.

Le nom de la caméra sert ensuite à créer un fichier JSON avec la classe "Sauvegarde", ce qui permet ultérieurement d'obtenir ces paramètres sans avoir à les recalculer.

class CameraParametre() :
    """Permet de stocker les paramètres de la caméra"""
    def __init__(self, nom, ret, mtx, dist, rvecs, tvecs, proj) :
        self.nom = nom
        self.ret = ret
        self.mtx = mtx
        self.dist = dist
        self.rvecs = rvecs
        self.tvecs = tvecs
        self.proj = proj
    
    def save_camera(self, chemin:str) :
        """sauvegarde les parametres de la camra dans le chemin donné"""
        Sauvegarde.save(self.cam_to_dic(), chemin + self.nom + ".json")

    def get_camera(chemin:str) :
       """obtient les parametres de la camra dans le présent dans le dossier donné"""
       return CameraParametre.from_dic(Sauvegarde.load(chemin))

# Code complet sur GitHub

Comme vous pouvez le voir, Nous faisons quelques fois appel à la Classe "Sauvegarde".

Cette classe contient uniquement des fonctions et procédures statiques.

Permettant de créer des fichiers JSON à partir d'un dictionnaire, ou d'obtenir un fichier à partir de son nom.

class Sauvegarde() :
    """permet de stocker une valeur à clef dans un fichier JSON"""
    # Cette classe contient des fonctions statiques qui permettent de stocker et récupérer de s valeurs dans un fichier JSON
    def save(donnee, path):
        with open(path, "w") as json_file:
            json.dump(donnee, json_file, indent=4)

    def load(path):
        with open(path, "r") as json_file:
            data = json.load(json_file)
        return data

Calibration d'une caméra

Une caméra permet de capturer un phénomène physique (la lumière) en donnée digitale. Malheureusement, le procédé du fonctionnement d’une caméra induit une inexactitude de ce à quoi l’image ressemble réellement à la réalité (distorsion, colorimétrie).

C’est ainsi que nous allons voir à partir de plusieurs images, comment nous pouvons en extraire des paramètres afin de calibrer la caméra et de réajuster ces images.

Paramètres d'une caméra

Une caméra peut être décrite avec plusieurs variables, que l’on appelle paramètre.

Ces paramètre se distinguent en deux catégories.

Les premiers sont les paramètre intrinsèques, qui sont les paramètres relatif à la caméra, les voici :

• Le centre optique, c'est le point théorique sur la caméra où les rayons lumineux convergent.

• La distance focale, est la distance entre le centre optique et l'objet sujet nécessaire à avoir une image nette.

• Les coefficients de distorsion, qui décrivent la distorsion radiale et tangentielle d'une image.

La deuxième catégorie sont les paramètres extrinsèques, qui correspondent à des valeurs inhérentes à l’image prise par la caméra. Ce sont donc des valeurs qui varient en fonction de la prise :

• Un vecteur de translation, qui représente la position de la caméra par rapport au sujet plan.

• Un vecteur de rotation, qui représente la rotation de la caméra par rapport au sujet plan.

Nous voulons donc dans un premier temps trouver ces paramètres.

Pour trouver ces paramètre, nous allons faire ce que l'on appelle un calibrage.

Calibrage

Pour faire un calibrage, nous allons prendre un motif connu.

Car avoir un motif que l'on connaît va nous permettre de "trouver les différences" entre l'image et la réalité, afin d'en extraire des paramètres.

Puisque si l'on sait qu'une ligne est droite dans la réalité mais qu'elle est courbée dans l'image, c'est qu'il y a eu une distorsion radiale.

Ou alors si deux lignes de même longueurs apparaissent de taille différentes, c'est que le plan est incliné par rapport à la caméra.

Nous allons donc prendre un damier. L'avantage du damier est que nous connaissons le nombre de carreaux et nous savons que ces carreaux sont bien droits (sans courbure).

Nous allons maintenant prendre en photo ce damier sous différents angles, ce qui va permettre à OpenCV d'estimer les paramètres de la caméra.

Voici les photos que j'ai prises :

Notons que plus nous allons donner d'images à OpenCV, plus les paramètres que l'on va obtenir vont être précis.

Mais que pour des soucis de performance, j'en ai fait que 3.

Maintenant que nous avons nos images, nous pouvons appelé ret, corners = cv.findChessboardCorners(gray, (7, 7), None)

Si ret vaut True après l'appel de cette fonction, c'est que OpenCV à trouvé le damier.

Dans ce cas, nous pouvons ajouter dans une liste les points objets (position des corner dans l'espace 3D) et les points images (ces même points sur l'image donc en 2D).

A partir de maintenant, nous pouvons appeler ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

Cette fonction est la fonction d'OpenCV qui va calculer les paramètres de la caméra.

Elle renvoi donc :

• ret : True ou False en fonction de si la calibration a fonctionnée.
• mtx : Appelé "Matrice de Caméra" Elle contient les paramètres intrinsèques, sauf les coefficients de distortions.

$camera\;matrice=\left[{\begin{matrix}f_{x}&0&c_{x}\\0&f_{y}&c_{y}\\0&0&1\end{matrix}}\right]$

• dist: Contient les coefficients de distortions.
• tvecs : Contient une liste de de vecteur, représentant la translation de la caméra par rapport à chaque image.
• rvecs : Contient une liste de de vecteur, représentant la rotation de la caméra par rapport à chaque image.

Notons que tvecs et rvecs sont généralement par la suite condensé dans ce qu'on appelle une matrice de projection, mais nous y reviendrons plus tard.

Pour la suite, étant donné que ma caméra ne fait pas subir de grosse distorsion à mes images. Je vais utiliser des images prisent d'internet pour illustrer mes propos.

Image de damier bien distordue, Prise sur internet

Grâce à ça, nous pouvons reconstruire l'image, sans la distorsion et autre effets de découlant la caméra.

Mais subsiste un problème. Lorsque nous allons dé-distosionner l'image, des zones noirs vont apparaître car l'image recourbé va laisser place à du vide.

Nous allons donc recalculer une matrice de caméra, spécifiquement conçu pour la résolution de l'image sans le noir.

newcameramtx, roi = cv.getOptimalNewCameraMatrix(camera.mtx, camera.dist, (w,h), alpha, (w,h))

Nous pouvons avec cette nouvelle matrice, dé-distorsionner l'image grâce au code : dst = cv.undistort(img, camera.mtx, camera.dist, None, newcameramtx)

À gauche, image dé-distortionnée avec la nouvelle matrice. À droite avec l'ancienne

Nous voyons donc bien l'importance de la calibration. Sans elle nous travaillerons sur des images complètement infidèles à la réalité.

Matrice de projection

Je vous parlais précédemment des paramètre intrinsèques et extrinsèques d'une caméra. Eh bien en réalité il est rare qu'on utilise ces données de façon brute.

En effet, nous allons généralement plutôt les condenser dans ce qu'on appelle une matrice de projection (noté P).

Une matrice de projection est donc une matrice qui contient les paramètres intrinsèques et extrinsèques d'une caméra.

Ce qui permet de savoir comment se place la caméra dans l'espace 3d + les distorsions induite par la caméra.

${\begin{pmatrix}u\\v\\1\end{pmatrix}}={\begin{pmatrix}f_{x}&0&c_{x}\\0&f_{y}&c_{y}\\0&0&1\end{pmatrix}}{\begin{pmatrix}r_{11}&r_{12}&r_{13}&t_{1}\\r_{21}&r_{22}&r_{23}&t_{2}\\r_{31}&r_{32}&r_{33}&t_{3}\end{pmatrix}}{\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}}$

Nous obtenons donc cette matrice en convertissant d'abord les rotation en Quaternion en Rodrigues.

Puis en faisant le produit matricielle de la matrice de caméra, et la matrice recomposé des paramètres extrinsèques

Cette matrice ayant 12 degrés de liberté, lesquels sont les 3 axes de rotation (* 3 car en Rodrigues) et les 3 axes de translation.

Les degrés de liberté étant des paramètres indépendants nécessaires pour spécifier complètement l'état d'un système.

Voyons voir maintenant, comment à partir des paramètres que l'on a extrait précédemment, comment nous pouvons établir cette matrice de projection.

matrice_rotation, _ = cv.Rodrigues(rvecs[i])
proj = np.dot(mtx, np.hstack((matrice_rotation, tvecs[i])))
matrices_proj.append(proj)

On pourrait maintenant à partir de cette matrice, faire de la réalité augmentée dans le cas où nous avons un motif prédéfinis tel que le damier.

Maintenant que nous avons vu les différentes étapes de calibration d'une caméra, voyons ce quels traitements nous pouvons donner aux images.

*Le code complet des 3 dernière sous parties se trouvent dans main.py sur GitHub.

Analyse et traitement d'une image

Tout d'abord, qu'est ce qu'une image.

Eh bien une image est juste une représentation visuelle, de données numérique plus complexe.

Ces données numérique varient en fonction du format de l'image. Mais contiennent en général des informations sur la résolution de l'image, la valeur RGB de chaque pixel et encore d'autres information.

Ainsi, comment l'ordinateur peut-il trouver des caractéristiques définissant une image afin de lui apporter des modifications ?

Nous allons pour cela, tenter de reconstituer un panorama à partir de ces deux images :

Trouver des descripteurs avec SIFT

Alors, comment faire pour trouver des caractéristiques déterminant l'image ?

Pour cela il existe quelque méthode sur OpenCV tel que SIFT, ORB ou encore SURF. Qui sont des méthodes permettant d'extraire les points clés d'une image.

Nous allons nous concentrer sur SIFT.

Dans un premier temps, SIFT va essayer de trouver des points qui pourrait être résistant à des transformation tel que des rotation et translation.

Pour ce faire, SIFT va dans un premier temps passer l'image en noir et blanc. Et à partir de cette images, va générer des copies avec des paramètres différents :

• L'algorithme va faire varier la différence de Gauss (DOG), qui va faire ressortir les contours. On génère cela en appliquant un flou Gaussien sur l'image.
• L'algorithme va également altérer l'image en réduisant la résolution de l'image, avec N octaves.

N octaves signifiant que l'on va réduire l'image de 1 / 2 à 1 / 2^N. Donc une image de largeur 1024 sera réduite à 512, 256, etc...

Pour bien comprendre ces transformations, j'ai codé un algorithme qui va générer toutes ces variations d'images.

def difference_gaussienne(image, n_octaves, n_scales):
    """Cette fonction sert à comprendre comment SIFT fait pour trouver des points clés résistants
    On va altérer l'image avec différentes résolutions et différents niveau de flou, permettant d'identifier les points clés résistants.
    Je stock toutes les images de différent niveau de gauss et de résolution dans le dossier gauss"""
    image_grayscale = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    image_grayscale = np.float32(image_grayscale)
    gaussian_images = []

    k = 2 ** (1 / n_scales)
    if not os.path.exists("gauss"):
        os.makedirs("gauss")

    for octave in range(n_octaves):
        sigma = 1.6
        octave_images = []
        for i in range(n_scales + 3):
            image_blurred = cv2.GaussianBlur(image_grayscale, (0, 0), sigma)
            octave_images.append(image_blurred)
            sigma *= k

        gaussian_images.append(octave_images)
        image_grayscale = cv2.resize(image_grayscale, (image_grayscale.shape[1] // 2, image_grayscale.shape[0] // 2))

    dog_images = []
    for octave_idx, octave_images in enumerate(gaussian_images):
        octave_folder = os.path.join("gauss", f"octave_{octave_idx}")
        os.makedirs(octave_folder, exist_ok=True)

        dog_octave = [octave_images[i + 1] - octave_images[i] for i in range(len(octave_images) - 1)]
        for scale_idx, dog_image in enumerate(dog_octave):
            cv2.imwrite(os.path.join(octave_folder, f"scale_{scale_idx}.jpg"), cv2.normalize(dog_image, None, 0, 255, cv2.NORM_MINMAX))
        dog_images.append(dog_octave)

    return dog_images

# Code complet disponible sur GitHub dans le fichier Gauss.py

Ce code m'a permis de générer toutes les variations de l'image de l'immeuble. J'ai ensuite assemblé toutes les images sur un logiciel de traitement pour bien voir les différentes transformations.

Comme nous pouvons le constater, sur certaines variation de l'images des points ressortent (Toits de voiture, motifs sur les fenêtres, etc...).

Et c'est comme ça que SIFT va sélectionner ses points clés. C'est à dire en regardant où la différence de niveau de gris est la plus grande.

Maintenant, comment faire pour décrire ces points clés ?

On pourrait penser qu'il suffit de conserver les valeurs RGB des zones autours de points clés.

Mais cette méthode ne prend pas en compte les différences de luminosité, rotation et translation possibles entre les deux images.

SIFT va donc plutôt utiliser ce qu'on appelle un histogramme de gradient orienté (HOG).

---

Pour faire court, un histogramme de gradient orienté est un vecteur de taille 9, qui contient l'information de la direction et magnitude du gradient d'une cellule.

Une cellule (ou patch) étant une partie de l'image dont la taille est prédéfinie. En général on prend des cellules de 8x8 pixels.

Mais voyons pas à pas comment est construit cet histogramme de gradient orienté.

Dans un premier temps, on va donc diviser l'image en une multitude de patch.

Ensuite, nous appliquons deux filtres de SOBEL sur l'image : Un horizontal et un vertical. Ce qui va permettre de faire ressortir les contours dans l'image.

Nous pouvons maintenant parcourir chaque pixel de chaque patch pour trouver :

• La direction du gradient : C'est la direction vers laquelle le changement d'intensité est le plus grand depuis le pixel.

Ce seront des angles non signés, c'est à dire que on aura un angle entre [0°, 180°]. On peut la calculer θ = arctan2(Gx, Gy) Avec Gx le pixel sur le filtre de Sobel horizontal, et Gy sur le vertical.

• La magnitude du gradient : il représente la norme du gradient. Plus la variation d'intensité est grande, plus la magnitude le sera.

On peut la calculer M = sqrt(Gx ** 2 + Gy ** 2)

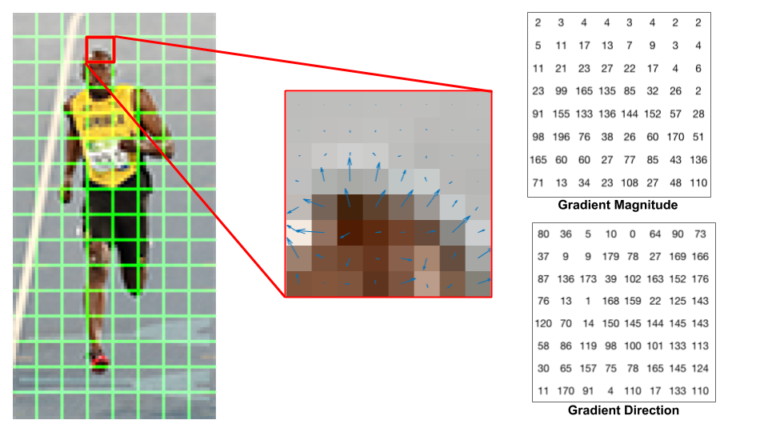
Voici un schéma, pris sur internet, qui exprime bien visuellement les valeurs que nous possédons en l'état.

Comme vous pouvez le voir. On a bien sur chaque pixel une flèche, dont la direction représente la direction du gradient et la norme la magnitude.

Il nous reste maintenant à calculer l'histogramme de ce patch.

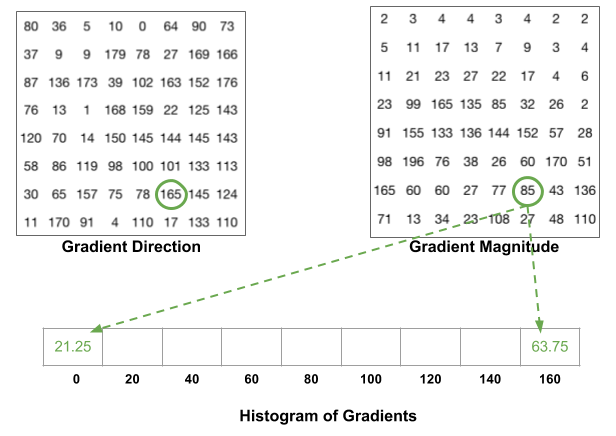
Pour ce faire, nous allons construire un histogramme de 9 bins. Chaque bins étant un multiple de 20 de 0 à 160. Qui est une répartition de l'angle.

Nous allons maintenant pour chaque pixel du patch, regarder la valeur de la direction de son gradient. Puis nous regardons entre quels bins cette valeur se trouve.

Puis nous regardons la magnitude de ce pixel, et nous répartissons cette magnitude sur les deux bins borne en faisant une interpolation linéaire.

Par exemple, si un pixel a une direction de 10° et une magnitude de 70, il est à 50% de la distance du bins 0 et 20. Donc on donne 35 (50% de 70) au bins 0, et 35 au bins 20.

C'est donc grossièrement comme cela, que SIFT va décrire les points d'intérêts d'une image.

Mais à présent, maintenant que nous avons nos points d'intérêts sur nos deux images. Comment déterminer la relation géométrique entre ces deux images ?

C'est ce que nous allons voir.

Construction du panorama par homographie

Pour reconstruire notre panorama, il faut donc que nous sachions quels transformations géométriques permettent de passer une d'une image à la perspective de son homologue.

Nous appelons la relation géométrique entre ces deux images une homographie.

Une homographie est représenté par une matrice d'homographie noté H de forme 3x3 :

$H={\begin{pmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{pmatrix}}$

Avec ici chaque élément de la matrice représentant un paramètre de la transformation géométrique. Sauf le h33 qui est l'élément de normalisation de la matrice souvent égal à 1.

C'est donc une matrice avec 8 degrés de liberté.

Voici donc, comment avec les points clés des deux images nous permettent de calculer cette matrice :

H, _ = cv.findHomography(pts_src, pts_dst, cv.RANSAC, 5.0)

Avec :

• pts_src et pts_dst étant les points clés des deux images.
• <cv.RANSAC> Qui est un algorithme d'élimination de points aberrants que nous verrons juste après.

Maintenant que nous savons quelles relations géométriques unit nos deux images que pouvons nous faire ?

Et bien pas mal de chose ! Par exemple, nous pouvons aisément transformé l'image 1 du bâtiment pour qu'elle soit à la perspective de l'image 2 :

Photo d'immeuble 1 remise à la perspective de l'image 2

Cela a été possible grâce à la méthode warpPerspective fournie par OpenCV :

hauteur, largeur, _ = img2.shape
img1_perspective = cv.warpPerspective(img1, H, (largeur, hauteur))

Avec cette matrice d'homographie, nous pouvons également tracer les lignes épipolaires.

Les lignes épipolaires sont les lignes fictive, reliant le centre optique de la caméra aux points de l'image 1 que l'on va tracer sur l'image 2.

Voici un exemple plus concret avec nos images d'immeuble :

Ligne épipolaires

Ces tracés sont utiles pour décrire visuellement le lien géométrique entre les deux images.

Maintenant, revenons à notre panorama.

Nous pourrions penser que pour reconstruire un panorama avec nos deux images il suffirait d'utiliser warpPerspective sur une des deux images puis de les assembler non ?

Alors oui et non. Car en plus de devoir mettre une image à la perspective de l'autre, il va falloir que nous les assemblions de tel sorte à ce que leur points de correspondance se supperposent.

Voici une des fonctions que j'ai codé me permettant justement de bien concaténer ces deux images en superposant le points de correspondance.

Cette fonction va aussi nous afficher avec des Gizmos quels points de correspondance sont utilisés pour la superposition.

def relie_point_correspondance(img1, keypoints1, img2, keypoints2, matches):
  """Ce script permet d'entourer et de relier tous les points de correspondance entre deux images"""

  # On créer une image vide permettant d'accueilir les deux images.
  r, c = img1.shape[:2]
  r1, c1 = img2.shape[:2]
  output_img = np.zeros((max([r, r1]), c+c1, 3), dtype='uint8')
  output_img[:r, :c, :] = np.dstack([img1, img1, img1])
  output_img[:r1, c:c+c1, :] = np.dstack([img2, img2, img2])

  # On parcours tous les points de correspondance, et on entoure chacun d'eux tout en les reliant à leurs homologues.
  for match in matches:
    img1_idx = match.queryIdx
    img2_idx = match.trainIdx
    (x1, y1) = keypoints1[img1_idx].pt
    (x2, y2) = keypoints2[img2_idx].pt

    cv2.circle(output_img, (int(x1),int(y1)), 4, (0, 255, 255), 1)
    cv2.circle(output_img, (int(x2)+c,int(y2)), 4, (0, 255, 255), 1)

    cv2.line(output_img, (int(x1),int(y1)), (int(x2)+c,int(y2)), (0, 255, 255), 1)
    
  return output_img

Voici donc les points qui vont servir à la superposition (correspondance entourées en rose sur la droite de l'image) :

Photo d'immeuble 1 remise à la perspective de l'image 2

Grâce à l'alliage de cette fonction et de warpPerspective nous pouvons ainsi reconstruire notre panorama.

(Code de la reconstruction de panorama disponible sur panorama.py du projet GitHub)

Photo d'immeuble 1 remise à la perspective de l'image 2

Reconstruction 3D

Nous allons maintenant nous intéresser à la reconstruction 3D. Qui est un domaine très important notamment dans le monde de la cinématographie ou dans le monde du jeu vidéo.

Nous pourrons ainsi comprendre, comment le Titanic à été remodélisé grâce à des photos pour le film éponyme.

Comment estimer la profondeur

Lorsque nous prenons un objet en photo sous plusieurs angle. Comment faisons nous pour dissocier l'objet au premier plan de l'arrière plan.

C'est à dire, comment pouvons nous estimer la distance de chaque points de l'image à la caméra.

Pour répondre à cette question, observons un phénomène de la vie courante.

Vous prenez le train et regardez par la fenêtre. Que remarquez vous ?

Et bien l'on remarque que plus un objet est proche, plus il va défiler rapidement devant nous. (arbres, maisons)

Tout comme plus l'objet est loin, plus il restera longtemps dans notre champs de vision. (montagnes, nuages)

Ce concept s'appelle la parallaxe. Nous pouvons donc nous baser sur ce dis concept pour estimer la distance de chaque objet dans la scène.

Par exemple, en prenant deux photos dont la seule différence est une translation de la caméra sur l'axe x.

Nous trouvons ainsi que les objets ayant le plus "bougé" sur l'axe x sont donc plus proche de la caméra.

Voici la formule qui décrit ce que nous venons d'expliquer : 'disparity = x − x′ = Bf / Z'.

Cette formule signifie juste que la profondeur d'un point est inversement proportionnelle à la distance sur l'axe x de ce même points entre deux images.

Cette relation se

Nous allons nous baser sur ce même concept

Sources : Wikipedia OpenCV doc learnopencv.com