Génération et résolution de labyrinthes
Aller à la navigation
Aller à la recherche
Approche mathématique des labyrinthes
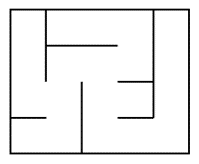
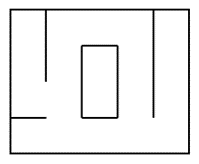
Un labyrinthe est dit parfait si chaque cellule est reliée à toutes les autres, et ce d’une seule manière. Les labyrinthes imparfaits peuvent donc contenir des boucles, des îlots ou des cellules inaccessibles
Nous nous intéresserons aux labyrinthes parfaits. On peut modéliser leurs chemins par des graphes. Pour résumer, un graphe est un ensemble de sommets reliés par des arrêtes.
Génération de labyrinthes
La création d'un labyrinthe suit les étapes suivantes :
- Générer un graphe G représentant une grille de taille m*n
- Construire un arbre couvrant A de ce graphe
- Dessiner le labyrinthe en traçant un mur entre les sommets directement liés dans G et non dans A
Qu'est ce qu'un arbre couvrant ?
Un arbre est un graphe à la fois connexe et sans cycle. Un arbre couvrant d'un graphe est un arbre inclus dans ce graphe et qui connecte tous les sommets du graphe.
Algorithmes de construction de l'arbre couvrant
Parcours en largeur du graphe G
On commence par explorer un nœud source, puis ses voisins, puis les voisins non explorés de ces voisins, etc
=Parcours en profondeur du graphe G
from collections import deque
def makeMaze(n, m, k):
"""
n : largeur
m : hauteur
k : nombre d'arêtes à retirer
"""
# génération de la grille
g = graphs.GridGraph([n,m])
g.set_pos( { (x,y) : (x,y) for (x,y) in g.vertices() } )
# suppression d'arêtes choisies aléatoires
for i in range( k ):
x = randint(0, n-1)
y = randint(0, m-1)
A = (x, y)
if randint( 0, 1 ) == 0:
B = (x+1, y)
else:
B = (x, y+1)
g.delete_edge(A, B)
return g
def drawMaze(g):
im = Graphics()
for (x,y) in g.vertices():
# draw walls
north = not g.has_edge((x,y), (x,y+1))
south = not g.has_edge((x,y), (x,y-1))
east = not g.has_edge((x,y), (x-1,y))
west = not g.has_edge((x,y), (x+1,y))
if north:
im += line([(x-0.5, y+0.5), (x+0.5, y+0.5)], rgbcolor=(0,0,0))
if south:
im += line([(x-0.5, y-0.5), (x+0.5, y-0.5)], rgbcolor=(0,0,0))
if east:
im += line([(x-0.5, y-0.5), (x-0.5, y+0.5)], rgbcolor=(0,0,0))
if west:
im += line([(x+0.5, y-0.5), (x+0.5, y+0.5)], rgbcolor=(0,0,0))
return im
def parcoursLargeur(G):
vu = set()
L = deque() # insérer : L.append( ), retirer : L.popleft()
A = Graph()
A.add_vertices( G.vertices() )
A.set_pos( G.get_pos() ) # juste pour l'affichage
s = (0,0)
vu.add(s)
L.append(s)
while len(L)>0:
u = L.popleft()
for v in G.neighbors(u):
if v not in vu:
A.add_edge(u, v)
L.append(v)
vu.add(v)
return A
def listerLesAretes(G):
for (u,v) in G.edges(labels=False):
print( "Arête : {}".format((u,v)) )