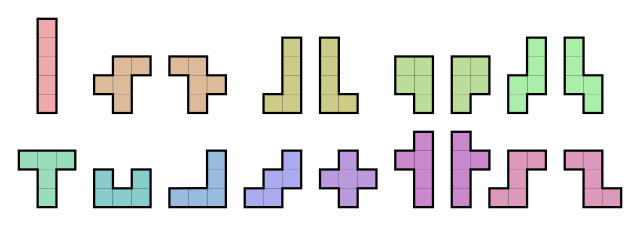VISI401 CMI : bibliographie scientifique

De Wiki du LAMA (UMR 5127)
Aller à la navigation Aller à la recherche

Responsable: Jacques-Olivier Lachaud

Ce module amène l'étudiant à effectuer des recherches bibliographiques sur un sujet donné, et à synthétiser ses résultats sous la forme d'un exposé construit.

L'étudiant, à partir d'un sujet et d'un ou plusieurs articles initiaux, doit approfondir le sujet, appréhender son historique, ses évolutions, et son état actuel.

A côté des ressources fournies par les bibliothèques, quelques pointeurs très utiles pour faire des recherches bibliographiques:

La synthèse bibliographique se fait en interaction avec le tuteur par des visites régulières et/ou des compte-rendus d'avancement par email. La synthèse finale fait l'objet d'un exposé final (15-20 minutes + questions) et d'un document de présentation.


sujets 2020-2021

Comment Facebook gère ses données ?

  • Tuteur : François Boussion
  • Résumé : Pour une base de données, il est impossible d'être cohérent, disponible tout le temps et partitionné. C'est le fameux théorème CAP. Pour autant, les données de Facebook sont cohérentes, disponibles tout le temps, et réparties à travers le monde !? Impossible. Pour l'étudiant, il faudra comprendre pourquoi c'est impossible, et comment Facebook fait en pratique pour gérer ce problème.
  • Objectifs :
    1. Comprendre le CAP théorème, et sa démonstration
    2. Comprendre comment Facebook gère ce problème, et ses données d'une manière générale
    3. À définir, selon les questions que se pose l'étudiant.
  • Références :
    1. Théorème CAP :
    1. Facebook Social Graph :
      1. TAO : The power of the graph (lien)
      2. TAO: Facebook’s Distributed Data Store for the Social Graph (lien)

Algorithmes de calcul de l'enveloppe convexe

  • Tuteur : Jacques-Olivier Lachaud
  • Résumé : Les ensembles convexes ont beaucoup de propriétés géométriques intéressantes, par exemple détecter la collision de deux ensembles convexes est "facile" algorithmiquement. Une étape fréquente dans beaucoup d'algorithmes de traitements de données 2D/3D/nD est donc de calculer l'enveloppe convexe d'un nuage de points, c'est-à-dire le plus petit ensemble convexe contenant ces points. Il existe de nombreux algorithmes de calcul d'enveloppe convexe en 2D (Graham scan, Melkman, balayage de ligne (sweep-line), division-fusion, Chan's algorithm, Quickhull) et 3D (Chan's algorithm, Quickhull) et même nD (Quickhull notamment).
Qhull-25.png
Enveloppe convexe des points à coordonnées entières inclus dans une boule de diamètre 25
  • Objectifs: il s'agira de regarder quelques uns de ces algorithmes, d'identifier leurs principales différences ainsi que leurs complexités théoriques et pratiques. On pourra aussi regarder plus précisément l'algorithme Quickhull, dont l'implémentation 2D est facile, et 3D accessible.
  • Bibliographie initiale :
    1. Barber, C. B., Dobkin, D. P., & Huhdanpaa, H. (1996). The quickhull algorithm for convex hulls. ACM Transactions on Mathematical Software (TOMS), 22(4), 469-483 [(PDF)]
    2. [Algorithme de Graham (Wikipedia)]
    3. [Convex hull algorithms (Wikipedia)]

Algorithmes autour des polyominos

  • Tuteur : Pierre Hyvernat
  • Résumé : Un polyomino est une forme (sans trou) obtenue en collant des petits carrés de taille 1 par leurs bords. Des exemples connus sont par exemples les pièces du jeu tetris : il s'agit de "tétramino", c'est à dire de polyomino formés de 4 carrés. Voici également les pentaminos, composés de 5 carrés :

Polyominos.png

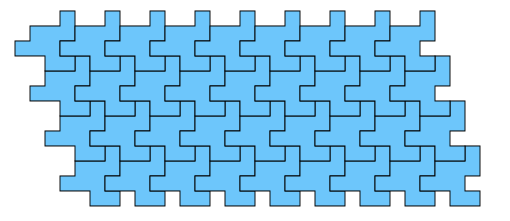
Une question récurrente est celle de la pavabilité : peut-on (en utilisant certains types de polyominos) paver un domaine donné. Lorsque le domaine est fini, on peut utiliser une recherche exhaustive, mais lorsqu'on veut paver tout le plan, le problème devient indécidable en général. Nous nous intéresserons au cas le plus simple : est-il possible de paver le plan tout entier en utilisant des polyominos tous identiques, et en utilisant uniquement des translations.

Pavages.png

  • Objectifs
    1. comprendre les définitions et notions de bases des polyominos, et en particulier leur représentation comme mot de contour
    2. implémenter différents algorithmes de reconnaissance de polyominos en Python
    3. comprendre la caractérisation des polyominos "exacts", càd ceux qui pavent le plan
    4. implémenter différents algorithmes de reconnaissance des polyominos exacts en Python


travaux réalisés 2019-2020

  • Crypto-système de Merkle-Hellman et algorithme de Shamir, Ewan Rakotoanosy (Tuteur : Pierre Hyvernat)
  • Reconstruction de surfaces à partir de nuages de points et de normales, Yohan Thépaut (Tuteur : Jacques-Olivier Lachaud)
  • Algorithmes de super-résolution par apprentissage, Romain Théodet (Tuteur : Jacques-Olivier Lachaud)
  • Autour de la question de la sensibilité des fonctions Booléennes, Christophe Carmagnac (Tuteur : Sébastien Tavenas)
  • Structures de données purement fonctionnelles, Loïc Dornel (Tuteur : Tom Hirschowitz)
  • Automates cellulaires et décidabilité, Lucas Chardonnet (Tuteur : François Boussion)

sujets 2019-2020

Crypto-système de Merkle-Hellman et algorithme de Shamir

  • Tuteur : Pierre Hyvernat
  • Résumé : Le système de Merkle-Hellman est un système cryptographique de type "clé publique / clé privée". Il a été inventé juste en 1978, après le système RSA (encore utilisé). Ce système a l'avantage d'être un peu plus simple, mais le **gros** désavantage d'avoir été craqué par A. Shamir en 1984. L'objectif est de comprendre le système, et la faille qu'il contenait. Cela permettra de comprendre l'algorithme de Shamir...
  • Bibliographie initiale :
    1. Shamir, Adi (1984). "A polynomial-time algorithm for breaking the basic Merkle - Hellman cryptosystem". IEEE Transactions on Information Theory. 30 (5): 699–704. doi:10.1109/SFCS.1982.5 [PDF]

Reconstruction de surfaces à partir de nuages de points et de normales

  • Tuteur : Jacques-Olivier Lachaud
  • Résumé : Les lasers d'acquisition de données 3d permettent de fabriquer des données qui approchent le bord d'un objet 3D. Ces données sont souvent sous la forme d'un nuage de points, doublé d'un vecteur associé à chaque point et qui indique la direction normale à la surface de l'objet. On parle de données de Hermite. Il existe des algorithmes dédiés, très efficaces et robustes, pour reconstruire une surface qui passe par ces points. L'objectif est de comprendre les deux principales méthodes, l'une appelée reconstruction de Poisson, l'autre relié à la notion d'indice (ou winding number), leurs qualités et leur défaut.
  • Bibliographie initiale:
    • KAZHDAN, Michael, BOLITHO, Matthew, et HOPPE, Hugues. Poisson surface reconstruction. In : Proceedings of the fourth Eurographics symposium on Geometry processing. 2006 [PDF]
    • BARILL, Gavin, DICKSON, Neil G., SCHMIDT, Ryan, et al. Fast winding numbers for soups and clouds. ACM Transactions on Graphics (TOG), 2018, vol. 37, no 4, p. 43. [[1]]

Algorithmes de super-résolution par apprentissage

  • Tuteur : Jacques-Olivier Lachaud
  • Résumé : La super-résolution consiste à, étant donné une image M x N, de fabriquer une image "zoomée" de taille kM x kN, où l'information inventée est "crédible". Le problème est évidemment mal posé mathématiquement, et du coup on rajoute de l'information a priori : continuité des couleurs, continuité des structures géométriques, modèles probabilistes, moyennes non-locales (auto-similarités), etc. Avec l'avènement du deep learning, des méthodes à base d'apprentissage ont vu le jour. En gros, un réseau de neurones (CNN) apprend sur plein d'images en "dézoomant" les images en entrées (facile, on sous-échantillonne), puis on utilise la fonction construite pour faire la super-résolution.
  • L'objectif est de regarder les méthodes de super-résolution, notamment celles par apprentissage et de voir leurs qualités et défauts. On pourra aussi les comparer avec des méthodes purement géométriques de super-résolution, ou des méthodes de moyennes non-locales.
  • Ce sujet a été discuté avec Romain Théodet et conduit à un stage au LAMA pour combiner méthode géométrique et méthode par deep learning pour la super-résolution.
  • Bibliographie initiale :
    • SHI, Wenzhe, CABALLERO, Jose, HUSZÁR, Ferenc, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In : Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. p. 1874-1883 [PDF]?
    • Lachaud, J.-O. and Kerautret, B., Geometric Total Variation for image vectorization, zooming and pixel art depixelizing, In : Proceedings of 5th Asian Conference on Pattern Recognition, 2019 Fichier:Paper-GTV.pdf
    • [Démos en ligne d'algorithmes de super-résolution]

Autour de la question de la sensibilité des fonctions Booléennes

  • Tuteur : Sébastien Tavenas
  • Résumé : On souhaite s’intéresser aux problèmes résolus par des algorithmes qui répondent par Vrai/Faux. Ces problèmes ont des entrées dans {0,1}^n (entrées codées en binaire) et une sortie dans {0,1) (Vrai ou Faux). Il est donc naturel de s’intéresser aux propriétés de ces fonctions Booléennes. Un certain nombre de paramètres intéressants ont été identifiés, comme la complexité du certificat (nombre minimal de bits nécessaires pour connaître la valeur de sortie), le degré (degré d’un polynôme qui correspond à la fonction sur les entrées Booléennes), la sensibilité (lnombre de bits qui, s’ils sont modifiés, impliquent une modification de la sortie), et bien d’autres (taille d’un arbre de décision, complexité en requêtes classiques ou quantiques, taille des coefficients de Fourier,…). En 1992, Nisan et Szegedy ont montré que tous ces paramètres sont reliés entre eux : si on connait l’un d’eux, par exemple le degré, on sait alors que n’importe quel autre de ces paramètres, par exemple la taille de l’arbre de décision, est limité à un certain intervalle de valeurs. Tous, sauf un : la sensibilité. Aucune méthode de preuve semblait impliquer que ce paramètre ne pouvait pas être beaucoup plus petit que les autres. Nisan et Szegedy posèrent alors la question de savoir si la sensibilité d’une fonction Bolléenne était reliée ou non aux autres paramètres classiques.
  • Cet été, en 2019, un chercheur, Hao Huang, a montré dans une preuve de deux pages que la sensibilité ne pouvait pas être significativement plus petite que les autres paramètres, résolvant le problème posé 27 ans auparavant. Cette "sensitivity" conjecture a été attaquée en vain par de nombreux chercheurs renommés. Or, la nouvelle preuve est si simple qu’un chercheur l’a résumé en un [tweet].
  • L'objectif est de comprendre quels sont les paramètres classiques des fonctions Booléennes et des liens entre eux avant de s'intéresser à la preuve de la conjecture. On pourra essayer de construire des fonctions extrémales (ie, avec des paramètres extrémaux dans leur plage de valeurs).
  • Bibliographie initiale :

Structures de données purement fonctionnelles

  • Tuteur : Tom Hirschowitz
  • Résumé : L'algorithmique est souvent enseignée sur des langages principalement impératifs tels que C. Les structures de données utilisées ne sont pas toujours évidentes à traduire vers les langages fonctionnels tels que OCaml. L'étudiant s'initiera aux structures de données fonctionnelles et aux concepts liés tels que la persistence, en suivant le livre « Purely functional data structures » d'Okasaki.
  • Liens

Automates cellulaires et décidabilité

  • Tuteur : François Boussion
  • Résumé : Un automate cellulaire est un modèle de calcul discret, utilisé en dans différentes sciences (informatique, mathématiques, physique, biologie, etc;). Le jeu de la vie est l'exemple emblématique d'automate cellulaire. Les règles de calcul d'un automate cellulaire, et de son évolution au cours du temps sont assez simples, mais mènent cependant à des problèmes complexes dont certains indécidables. Par exemple, déterminer si, étant donné des règles, on arrivera forcément, en un nombre fini d'étapes, dans une configuration donné, quelque soit la configuration initiale (problème de nilopotence).
  • L'objectif est de s'intéresser à ces problèmes indécidables dans les automates cellulaires et de produire un mini-cours sur le sujet.
  • Références
    • K. JARKKO, The nilpotency problem of one-dimensional cellular automata, SIAM J. Comput., Vol. 21, No. 3, pp. 571-586, June 1992.
    • K. CULIK II, J. PACHL, S. Yu, On the limit sets ofcellular automata, SIAM J. Comput., 18 (1989), pp.831-842.

travaux réalisés 2018-2019

Les exposés auront lieu le lundi 27 mai de 9h à 11h en salle 115 du chablais. Prévoyez 15-20min suivi de questions.

sujets 2018-2019

Les sujets 1-3 sont encadrés par J.-O. Lachaud, les sujets 4-5 par P. Hyvernat, le sujet 6 par S. Tavenas. Un encadrant encadre au max 2 étudiants.

  1. Débruitage de surfaces maillées (mesh denoising): Etant donné une surface triangulées, dont la position des sommets est "bruité" (en général par les moyens d'acquisitions utilisés pour la fabriquer), ces algorithmes tentent de retrouver la surface initiale, en supposant par exemple qu'elle était lisse ou lisse par morceaux.
    • Bilateral mesh denoising, S Fleishman, I Drori, D Cohen-Or - ACM transactions on graphics (TOG), 2003 - dl.acm.org
    • Mesh denoising via L0 minimization, L He, S Schaefer - ACM Transactions on Graphics (TOG), 2013 - dl.acm.org
    • Variational mesh denoising using total variation and piecewise constant function space, H Zhang, C Wu, J Zhang, J Deng - IEEE transactions on …, 2015 - ieeexplore.ieee.org
  2. Approximation de formes: il s'agit de fabriquer, à partir d'une surface maillée précise, une nouvelle surface composée de beaucoup moins de sommets qui l'approche et qui conserve ses caractéristiques principales. Cela sert aussi en compression de formes.
    • Progressive meshes, H Hoppe - Proceedings of the 23rd annual conference on SIGGRAPH, 1996 - dl.acm.org
    • Variational shape approximation, D Cohen-Steiner, P Alliez, M Desbrun - ACM Transactions on Graphics …, 2004 - dl.acm.org
  3. Reconstruction de surfaces à partir de nuages de points: il s'agit de trouver comment fabriquer une surface qui approche un ensemble de points dans l'espace.
    • Delaunay triangulation based surface reconstruction.F Cazals, J Giesen - Effective computational geometry for curves and …, 2006 - Springer
    • State of the art in surface reconstruction from point clouds, M Berger, A Tagliasacchi, L Seversky, P Alliez… - EUROGRAPHICS star …, 2014 - hal.inria.fr
    • Bayesian point cloud reconstruction, P Jenke, M Wand, M Bokeloh… - Computer Graphics …, 2006 - Wiley Online Library
  4. "dancing links" : l'algorithme X de Knuth est un algorithme élégant et "efficace" pour chercher une solution au problème combinatoire de la couverture exacte. Cet algorithme peut s'appliquer à des problèmes aussi divers que la résolution de sudoku ou le pavage par polyominos. Ce problème fait partie de la classe des problèmes NP-complets qui sont intrinsequement difficiles
    • "Dancing links" : description de l'algorithme X de Knuth et de quelques applications Millennial Perspectives in Computer Science : Proceedings of the 1999 Oxford-Microsoft Symposium in Honour of Sir Tony Hoare, Palgrave, coll. « Cornerstones of Computing », 2000
  5. Le langage LISP est un des plus vieux langages de programmation encore (un peu) utilisé. (LISP: 1958, C: 1972, Python: 1989). Il s'agit d'un langage fonctionnel avec une syntaxe très simple. La programmation fonctionnelle s'est ensuite developpé dans plusieurs directions, notamment avec la notion de typage fort (Hindley-Milner) utilisé par les langages de la famille ML (SML, Caml)
  6. Une question naturelle est de savoir quels sont les problèmes qui peuvent être résolus avec un espace mémoire restreint. Plus formellement, on notera L l'ensemble des problèmes que l'on peut résoudre en utilisant seulement un espace mémoire logarithmique. On s'intéresse à cette classe de problèmes, et plus particulièrement aux problèmes de connectivité dans un graphe.

travaux réalisés 2017-2018

Les exposés auront lieu le vendredi 25 mai 2018, à 9h. Prévoyez 15-20min suivi de questions.


sujets 2017-2018

  1. Du ray-tracing au path-tracing: il s'agit de comprendre l'évolution des algorithmes de rendu (dits "réalistes") et de mettre en avant les principales évolutions.
  2. Débruitage de surfaces maillées (mesh denoising): Etant donné une surface triangulées, dont la position des sommets est "bruité" (en général par les moyens d'acquisitions utilisés pour la fabriquer), ces algorithmes tentent de retrouver la surface initiale, en supposant par exemple qu'elle était lisse ou lisse par morceaux.
    • Bilateral mesh denoising, S Fleishman, I Drori, D Cohen-Or - ACM transactions on graphics (TOG), 2003 - dl.acm.org
    • Mesh denoising via L0 minimization, L He, S Schaefer - ACM Transactions on Graphics (TOG), 2013 - dl.acm.org
    • Variational mesh denoising using total variation and piecewise constant function space, H Zhang, C Wu, J Zhang, J Deng - IEEE transactions on …, 2015 - ieeexplore.ieee.org
  3. Approximation de formes: il s'agit de fabriquer, à partir d'une surface maillée précise, une nouvelle surface composée de beaucoup moins de sommets qui l'approche et qui conserve ses caractéristiques principales. Cela sert aussi en compression de formes.
    • Progressive meshes, H Hoppe - Proceedings of the 23rd annual conference on SIGGRAPH, 1996 - dl.acm.org
    • Variational shape approximation, D Cohen-Steiner, P Alliez, M Desbrun - ACM Transactions on Graphics …, 2004 - dl.acm.org
  4. Reconstruction de surfaces à partir de nuages de points: il s'agit de trouver comment fabriquer une surface qui approche un ensemble de points dans l'espace.
    • Delaunay triangulation based surface reconstruction.F Cazals, J Giesen - Effective computational geometry for curves and …, 2006 - Springer
    • State of the art in surface reconstruction from point clouds, M Berger, A Tagliasacchi, L Seversky, P Alliez… - EUROGRAPHICS star …, 2014 - hal.inria.fr
    • Bayesian point cloud reconstruction, P Jenke, M Wand, M Bokeloh… - Computer Graphics …, 2006 - Wiley Online Library
  5. "dancing links" et NP complétude : l'algorithme X de Knuth est un algorithme élégant et "efficace" pour chercher une solution au problème combinatoire de la couverture exacte. Cet algorithme peut s'appliquer à des problèmes aussi divers que la résolution de sudoku ou le pavage par polyominos. Ce problème fait partie de la classe des problèmes NP-complets qui sont intrinsequement difficiles
    • "Dancing links" : description de l'algorithme X de Knuth et de quelques applications Millennial Perspectives in Computer Science : Proceedings of the 1999 Oxford-Microsoft Symposium in Honour of Sir Tony Hoare, Palgrave, coll. « Cornerstones of Computing », 2000
    • Classic Nintendo Games are (Computationally) Hard : preuve que Super Mario et d'autres jeux video classiques sont NP-complets Theoretical Computer Science, volume 586, 2015, pages 135–160.
  6. Le langage LISP est un des plus vieux langages de programmation encore (un peu) utilisé. (LISP: 1958, C: 1972, Python: 1989). Il s'agit d'un langage fonctionnel avec une syntaxe très simple. La programmation fonctionnelle s'est ensuite developpé dans plusieurs directions, notamment avec la notion de typage fort (Hindley-Milner) utilisé par les langages de la famille ML (SML, Caml)
Récupérée de « http://os-vps418.infomaniak.ch:1250/mediawiki/index.php?title=VISI401_CMI_:_bibliographie_scientifique&oldid=12708 »