Les réseaux euclidiens
Un réseau euclidien est un objet mathématique qui a été utilisé premièrement pour la cryptanalyse. C'est Miklos Ajtai qui a démontré que les réseaux euclidiens peuvent servir de base solide pour la cryptologie. Certains caractéristiques remarquables des problèmes de réseaux sont qu'il n'y a pas d'instances faibles, ce qui ne va pas être le cas de RSA où avec certains nombres premiers la factorisation sera trop simple. De plus ces problèmes sont reconnu comme étant difficile. Il est donc pas possible de les résoudre efficacement. Et pour finir, on ne connaît pas d'attaque même avec un ordinateurs quantiques. Les cryptosystèmes qui se basent sur cet objet mathématique sont donc actuellement source de nombreuse études. En particularité pour la caractéristique homomorphe de ce chiffrement, c'est à dire qu'on peut effectuer des calculs directement sur le chiffré. Cela peut garantir la sécurité dans de nombreuses applications comme par exemple lors de calculs effectués sur les services cloud.
Les principes de base
Un réseau euclidien est un sous-groupe discret d'un espace vectoriel euclidien : un réseau euclidien est un ensemble de points régulièrement arrangés sur un plan ou sur une dimension plus grande. On peut faire des additions et des soustractions sur cet ensemble donc nous parlons bien d'un sous-groupe. ce sous-groupe est discret car bien que le nombre de points paraît être générable à l'infini, on peut les dénombrer et les indexer par des nombres entiers.
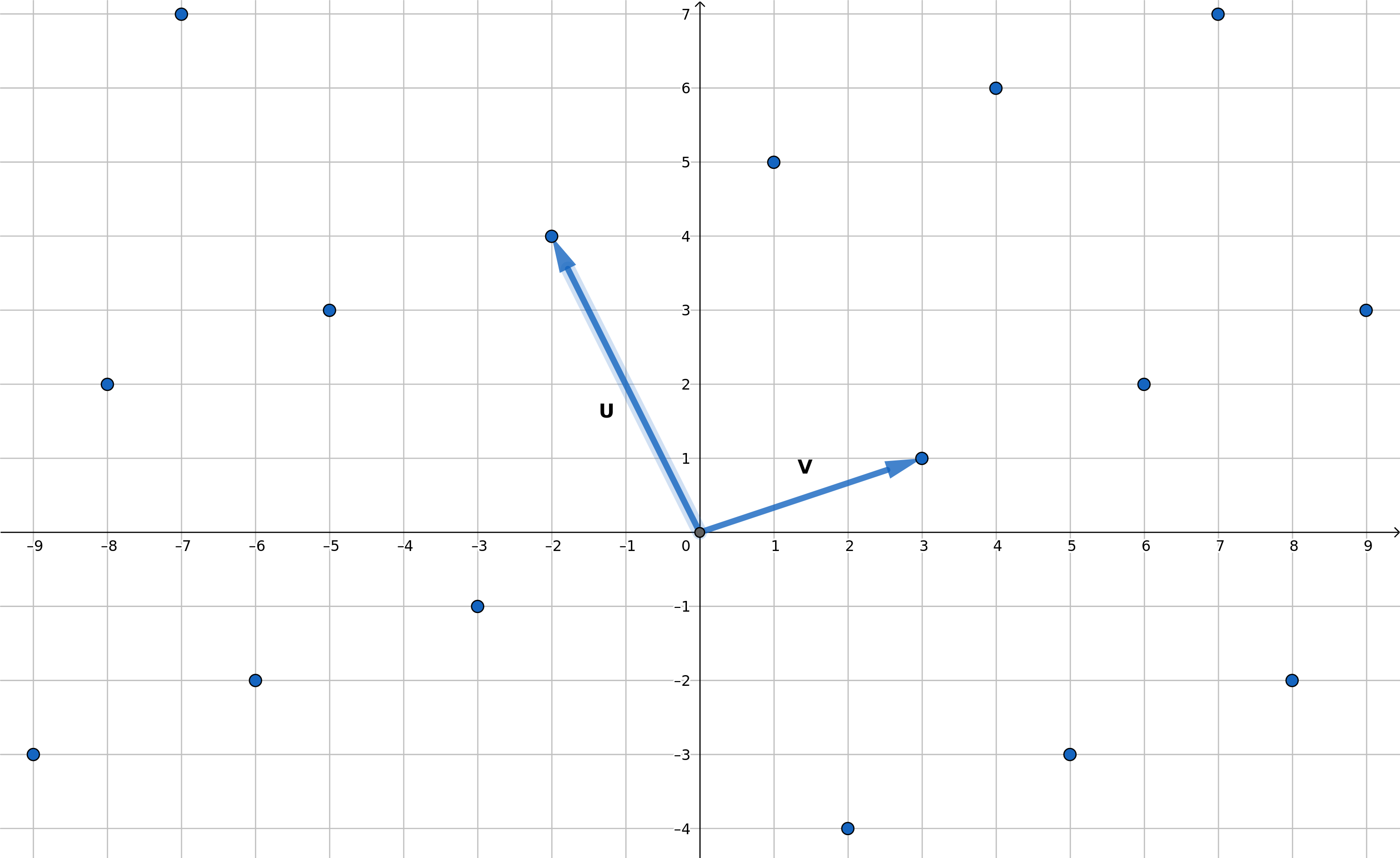
Voici la représentation d'un réseau euclidien de dimension 2. Comme le nombre de points est infini il serait difficile de faire la liste de ces points. Ils sont donc représentés par une base, ici (O, u, v). Les points ont donc des coordonnées correspondant à la base de notre réseau euclidien.
//Image
Base différentes
Un réseau euclidien peut être représenté par plusieurs bases sur, ici un plan (dimension 2). Les différence avec le système de coordonnées du plan (0,x,y) c'est que dans un réseau euclidien les coordonnées sont toujours des entiers et la base n'est pas nécessairement rectangulaire. //image