Transactions Bitcoins & Signatures numérique

Le Bitcoin est une monnaie numérique, ou cryptomonnaie, créer en 2009 par la personne ou le groupe de personne connues sous le pseudonyme de Satoshi Nakamoto. Une cryptomonnaie est une monnaie numérique, dématérialisée et sans organisme centralisé ou autorité centrale de régulation (banques). Le Bitcoin repose pour ce faire sur un réseau pair à pair et sur l'utilisation de la blockchain.

Blockchain

Registre des transactions

La blockchain se présente comme un réseau pair à pair dans lequel chacun des nœuds possède une copie du registre contenant l'intégralité de transactions de Bitcoin ayant eu lieu. Lorsqu'un utilisateur désir créer une nouvelle transaction, il lui suffit de l'ajouter dans le registre. Cette transaction va ensuite être propagée dans les nœuds voisins afin que chacun des nœuds ait la dite transaction inscrite dans son registre. Ainsi, les nœuds du réseau vont s'échanger en permanence les nouvelles transactions qui ont été créée dans leur registre ou qu'ils ont reçu depuis un autre nœud.

Elliptic Curve Cryptography

La cryptographie sur les courbes elliptiques (en anglais, elliptic curve cryptography ou ECC) regroupe un ensemble de techniques cryptographiques qui utilisent une ou plusieurs propriétés des courbes elliptiques. Les premières utilisations de ces courbes remontent en 1985 de manière indépendante par Neal Koblitz et Victor Miller.

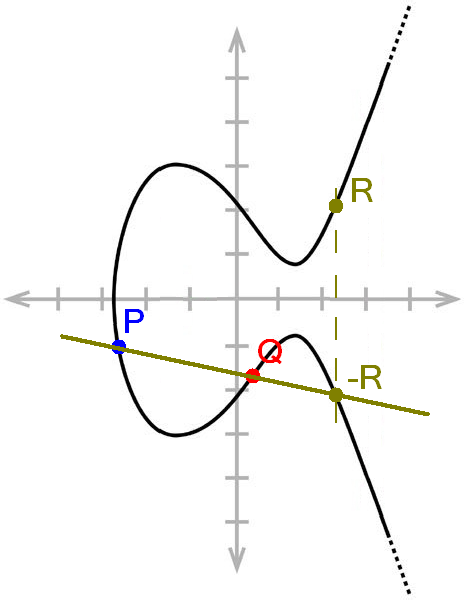
Propriétés utiles d’une courbe elliptique

- Une courbe elliptique est symétrique par rapport à l’axe des abscisses.
- Une droite passant par 2 points de la courbe coupe cette dernière en un 3ème points.

Ces deux propriétés nous permettent d'effectuer l'opération "dot" illustrée sur le schéma ci-contre qui nous sera très utile pour l'algorithme de signature.

Opération sur la courbe => P . Q -> R

Les plus de ECC

ECC permet de garantir la même sécurité que RSA mais avec des clés bien plus courte, ce qui permet d'améliorer les temps de calcul. Par exemple avec une clé ECC de 256 bits, on obtient la même sécurité que le système RSA avec un clé de 3072 bits. En allant un peu plus pour atteindre une sécurité dite "Top Secret" par la NSA le système ECC nécessite une taille de clé de 384 bits contre 7680 pour RSA.

Elliptic Curve Digital Signature Algorithm

Elliptic Curve Digital Signature Algorithm (ECDSA) est un algorithme de signature numérique à clé publique et privée. Cet algorithme se base sur la cryptographie sur les courbes elliptiques vu précédemment. Cet algorithme a été proposée pour la première fois en 1992 par Scott Vanstone.

Données d'entrée de ECDSA

- Formule de la courbe => y² = x³ + ax + b (courbe elliptique sur un corps d'entiers fini modulo p avec p un nombre premier).
- Un point de la courbe (appelé point de base) => G.
- L’ordre de G => n. Le plus petit entier tel que n . G donne O le point à l’infini de la courbe, pour que tous les entiers entre 1 et n-1 soit modulo n. De plus n doit être premier pour que l’anneau Z/nZ soit un corps. Ce nombre correspond au plus grand nombre possible pour une clé, l'ordre de n donne donc la taille de la clé.

Génération des clés

Chaque personne doit avoir une clé privée et une clé publique.

- Clé privée a : un nombre entre 1 et n-1.
- Clé publique A : a . G.

Signature

Pour signé :

- On choisit on nombre aléatoire k entre 1 et n - 1.
- On calcule le point K = k . G.
- On garde la composante $K_{x}$ qu'on appellera r.
- On calcule un nombre z qui correspond au résultat d'un hachage cryptographique sur le message à signer.
- On calcule ensuite un nombre $s=k^{-1}.(z+ra){\bmod {n}}$.
- La signature correspond au couple (r,s).

Vérification

Pour vérifier la signature :

- On calcul un nombre $w=s^{-1}{\bmod {n}}$.
- On calcul deux coefficients $u_{1}=zw{\bmod {n}}$ et $u_{2}=rw{\bmod {n}}$.
- On peut donc calculer ce qu'on appelle le point de vérification de la signature $S=u_{1}.G+u_{2}.A$

Pour les transaction BitCoin

La courbe utilisée pour le BitCoin est Secp256k1 dont l’équation est y² = x³ + 7. Cette courbe est utilisée pour des raisons de performance de calcul.

- Gx = 79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
- Gy = 483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
- n = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

Exemple de signature et vérificaction

Créer par Thomas De Iseppi et Flavien Stemmelen