Génération et résolution de labyrinthes II

Labyrinthe généré avec Kruskal et résolu avec le parcours en profondeur. En route foncé, l'entrée. En vert, la sortie. En bleu, le chemin. En rouge clair, les cellules visitées lors de la résolution.

Lorem ipsum

Représentation

Propriétés

Un labyrinthe est une grille de cellules reliées, ou non, entre elles.

Deux cellules sont reliées entre elles par une porte, ou séparées par un mur.

Tout labyrinthe a une entrée et une sortie, et quelle que soit l'entrée ou la sortie, le chemin entre ces deux cellules est unique.

Modélisation en graphe

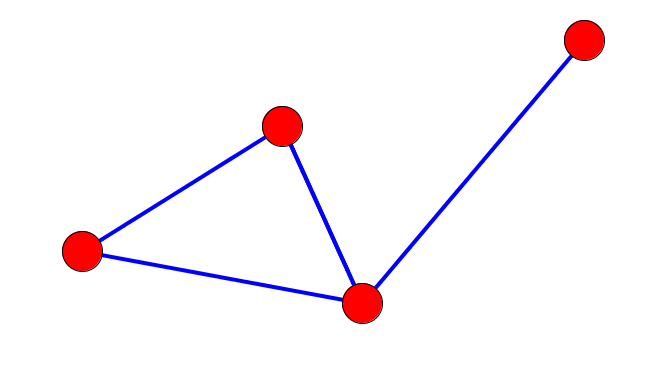
En théorie des graphes, un graphe est un ensemble de points (ou nœuds ou sommets) reliés ensemble par des lignes (ou liens ou arêtes).

Exemple de graphe connexe cyclique non orienté

Un graphe peut être connexe (en un seul morceau) ou non connexe (en plusieurs morceaux).

Un graphe peut aussi être cyclique si les points sont reliés en formant une boucle ou acyclique.

Enfin, un graphe peut être orienté (si les arêtes sont à sens unique) ou non orienté.

Exemple d'arbre

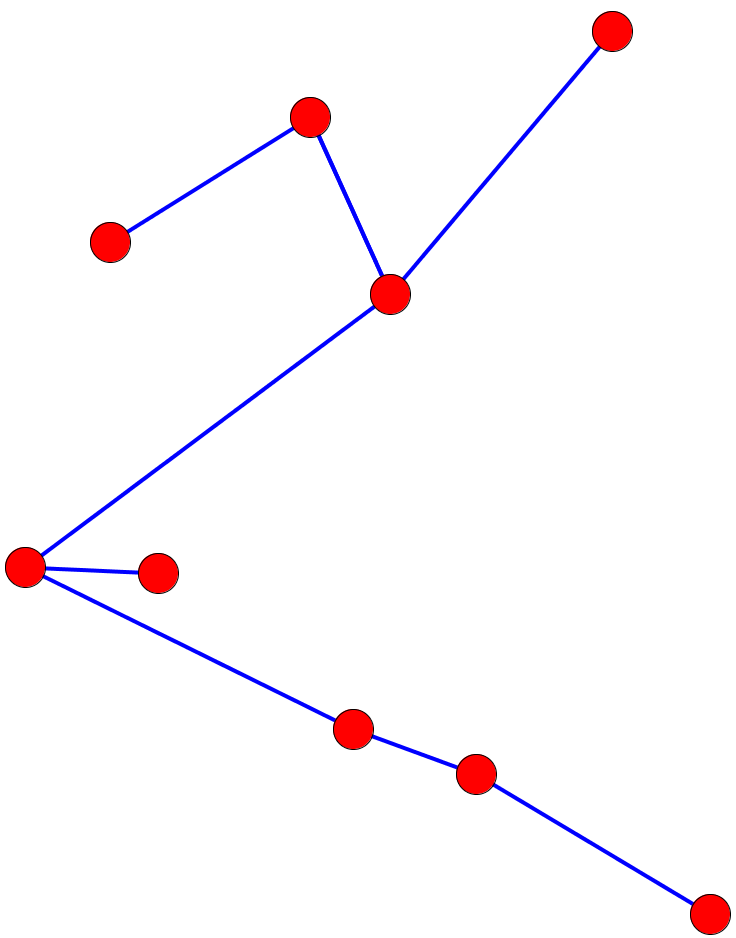
Un arbre est un graphe connexe, acyclique et non orienté.

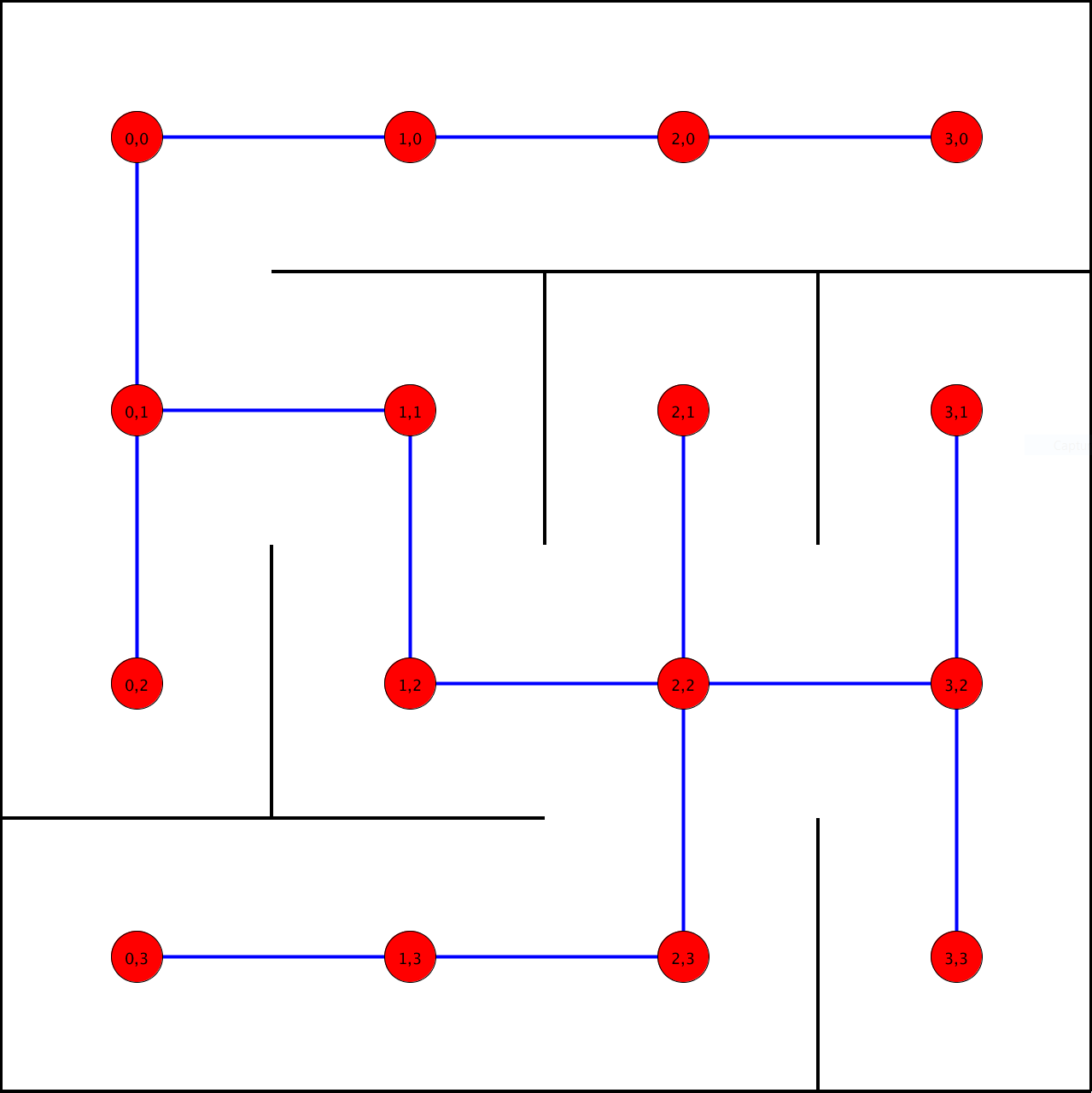
En plaçant un point sur chaque cellule de notre labyrinthe, et en reliant deux cellules séparées par une porte, on peut dessiner un arbre à partir de n'importe quel labyrinthe.

Exemple de labyrinthe avec son arbre. Pour plus de simplicité, on attribue à chaque nœud une position.

Génération

Un labyrinthe rectangulaire de largeur $L$ et de hauteur $H$ contient exactement $L\times H-1$ portes.

Du point de vue du graphe, il y a donc $L\times H-1$ arêtes.

Maintenant, comment répartir toutes ces portes de façon à ce que toutes les cellules soient accessibles et qu'il n'existe qu'un unique chemin entre l'entrée et la sortie ?

De nombreux algorithmes existent, dont le parcours en profondeur et l'algorithme de Kruskal. Chaque algorithme est différent et produit des labyrinthes visuellement différents.

Parcours en profondeur

Illustration du parcours en profondeur

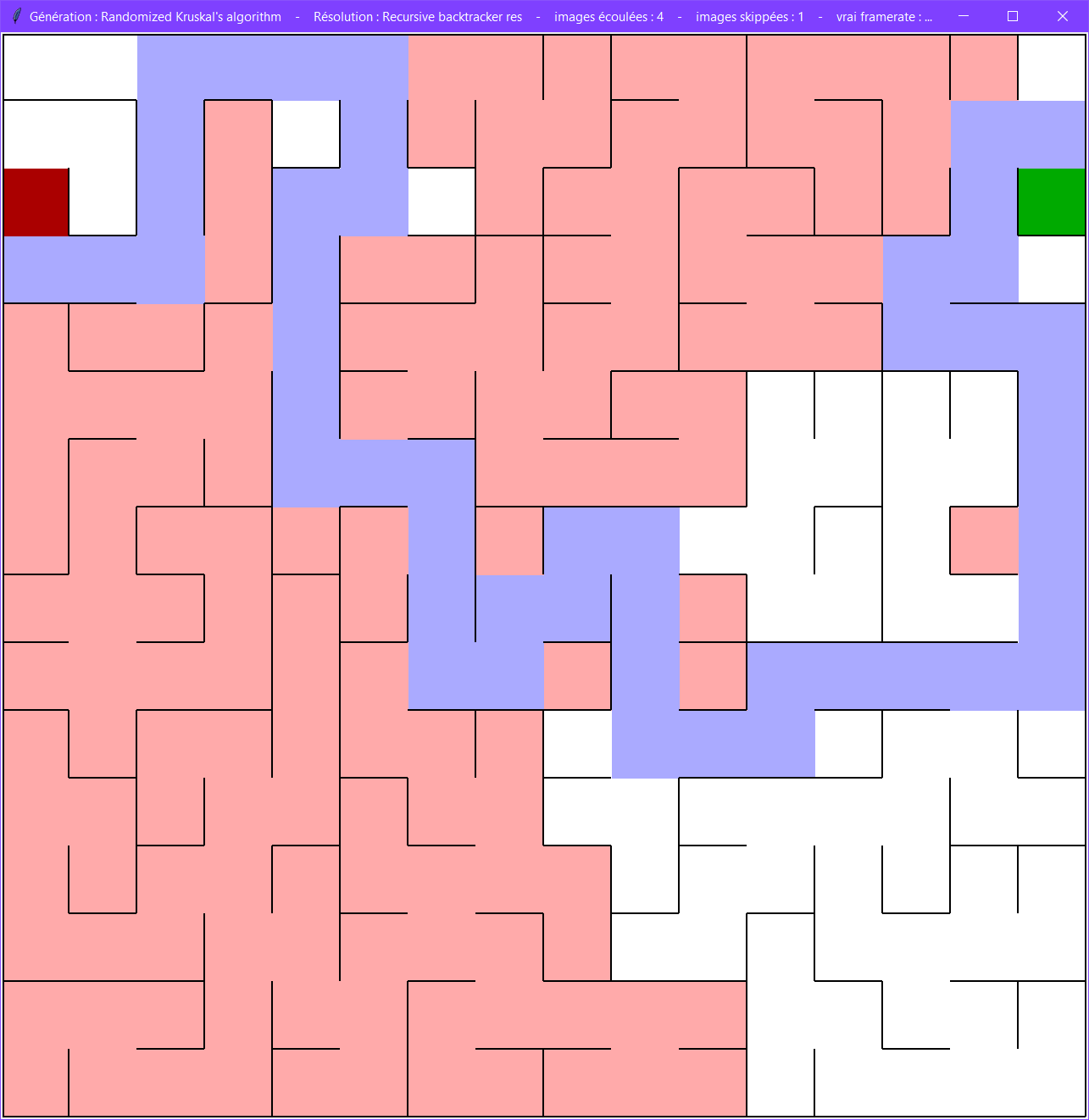
Dans l'algorithme du parcours en profondeur ("recursive backtracker" en anglais), on commence sur une cellule aléatoire dans le labyrinthe.

On se dirige dans une direction aléatoire et on casse le mur en face, tout en marquant la cellule précédente comme visitée.

Lorsque aucune direction n'est disponible, on remonte à la position précédente.

Représentation d'une pile de positions

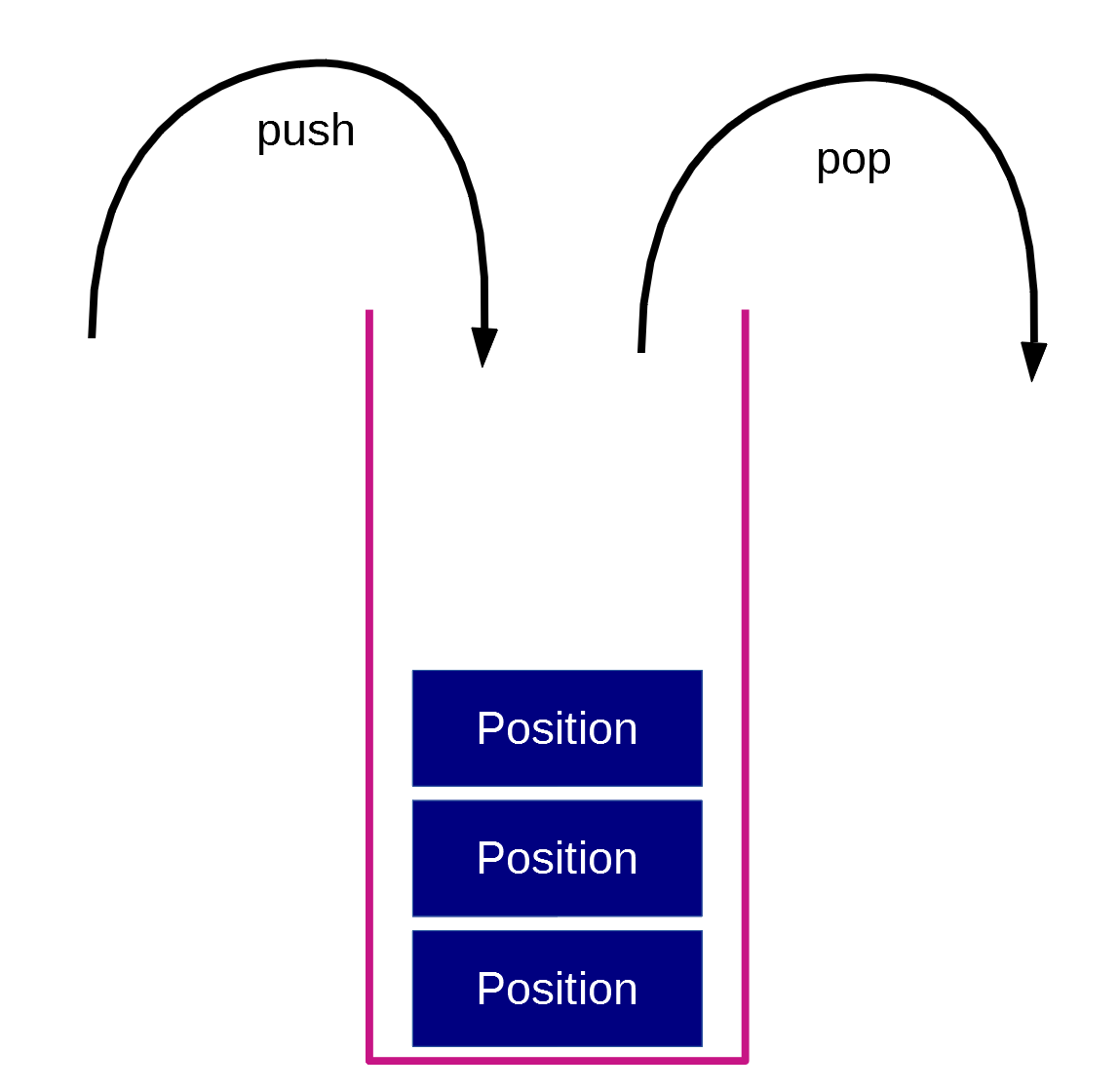
Pour sauvegarder l'historique des positions, on peut utiliser une pile.

Une pile est une liste dans laquelle seul le dernier élément peut être récupéré.

Une pile contient 2 méthodes :

• push(elem) : ajoute elem à la pile
• pop() -> elem : retourne le dernier élément de la pile (elem dans notre cas)

Dans mon implémentation de la pile, une erreur est levée si l'on appelle la méthode pop sur une pile vide.

Kruskal

Alors que pour le parcours en profondeur on partait des cellules, l'algorithme de Kruskal s'applique sur des murs.

On attribue à chaque cellule un identifiant unique.

On choisit

Labyrinthes cycliques

Il est possible, en retirant un certain pourcentage de murs, de créer des labyrinthes cycliques à partir des labyrinthes acycliques générés auparavant.

Cependant, certains algorithmes de résolution n'auront pas le même comportement.

Résolution

?

Affichage

tkinter

tkinter

Code

N'ayant pas utilisé de bibliothèques autres que tkinter, mon projet total contient plusieurs milliers de lignes réparties dans une dizaine de fichiers.

Je ne peux donc évidemment pas l'insérer directement dans cette page.

Le code source est disponible sur Github à cette adresse

Sources

Diapo INFO805

eee

T E S T