Génération et résolution de labyrinthes II
L’avènement de l’Internet des Objets (IoT) depuis une dizaine d’années a fait apparaitre des problématiques propres aux protocoles de communications liées à ces objets. En effet, l’échange de données dans ce contexte nécessite de tenir compte (au moins) des paramètres suivant :
- Autonomie énergétique souvent limitée
- Faible puissance des processeurs et taille réduite de la mémoire
- Disponibilité « aléatoire » de l’accès aux réseaux de communication
De nombreux protocoles cohabitent et la littérature du domaine foisonne d’exemples autour des réseaux dédiées (LORA, Sigfox, etc.) et des protocoles applicatifs (OPC-UA, MQTT, CoaP, XMPP) mais force est de constater que dans la réalité, ces solutions ne répondent pas toujours aux besoins des concepteurs qui leurs préfèrent encore le protocole HTTP. Celui-ci offre l’avantage d’implémenter un protocole applicatif (REST) en même temps qu’un protocole de transport de haut niveau (TCP/IP) permettant de passer les pare-feu. Cependant, la version actuel d’HTTP ne répond pas vraiment aux critères énoncés précédemment. Depuis quelques années émerge donc l’idée d’enrichir HTTP pour créer un protocole hybride qui mêlerait les avantages de REST avec ceux proposés par les mécanismes de type Publish/Subscribe (MQTT, AMQP, JMS, etc.). En attendant cette éventuelle évolution, peut-on envisager de mettre en place un mécanisme de type Pub/Sub avec le protocole Websocket au-dessus d’HTTP ?
Représentation
Propriétés
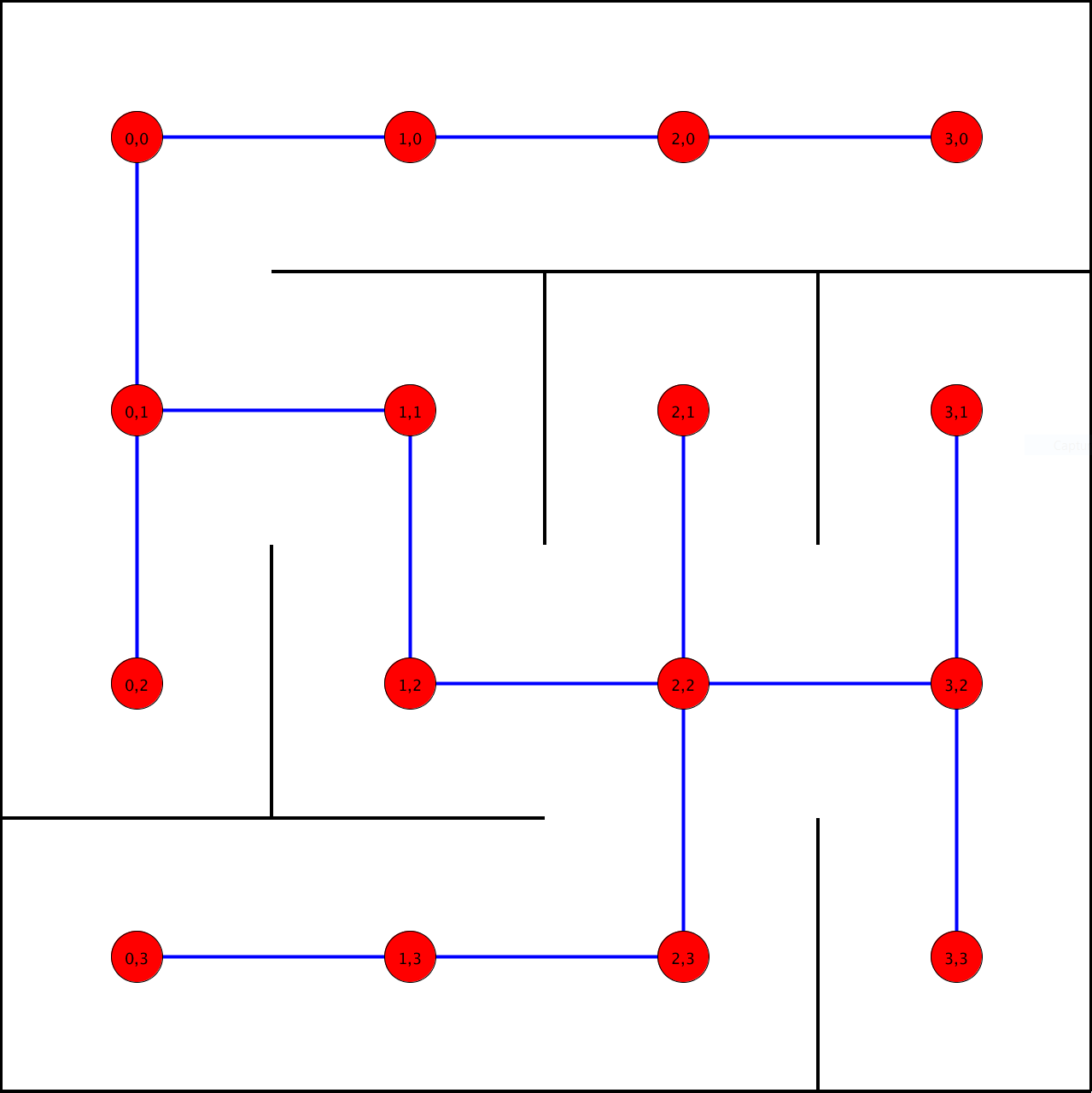
Un labyrinthe est une grille de cellules reliées, ou non, entre elles.
Deux cellules sont reliées entre elles par une porte, ou séparées par un mur.
Tout labyrinthe a une entrée et une sortie, et quelle que soit l'entrée ou la sortie, le chemin entre ces deux cellules est unique.
Modélisation en graphe
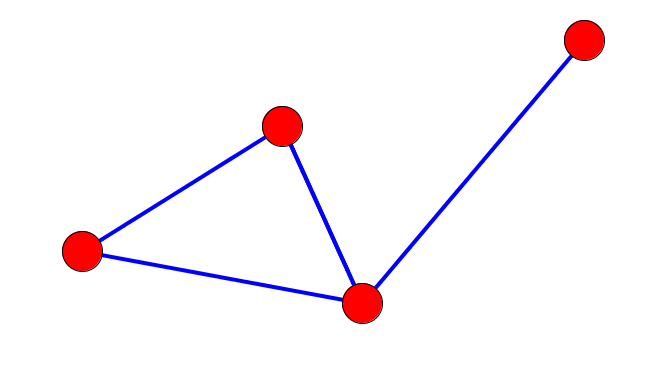
En théorie des graphes, un graphe est un ensemble de points (ou nœuds ou sommets) reliés ensemble par des lignes (ou liens ou arêtes).
Un graphe peut être connexe (en un seul morceau) ou non connexe (en plusieurs morceaux).
Un graphe peut aussi être cyclique si les points sont reliés en formant une boucle ou acyclique.
Enfin, un graphe peut être orienté (si les arêtes sont à sens unique) ou non orienté.
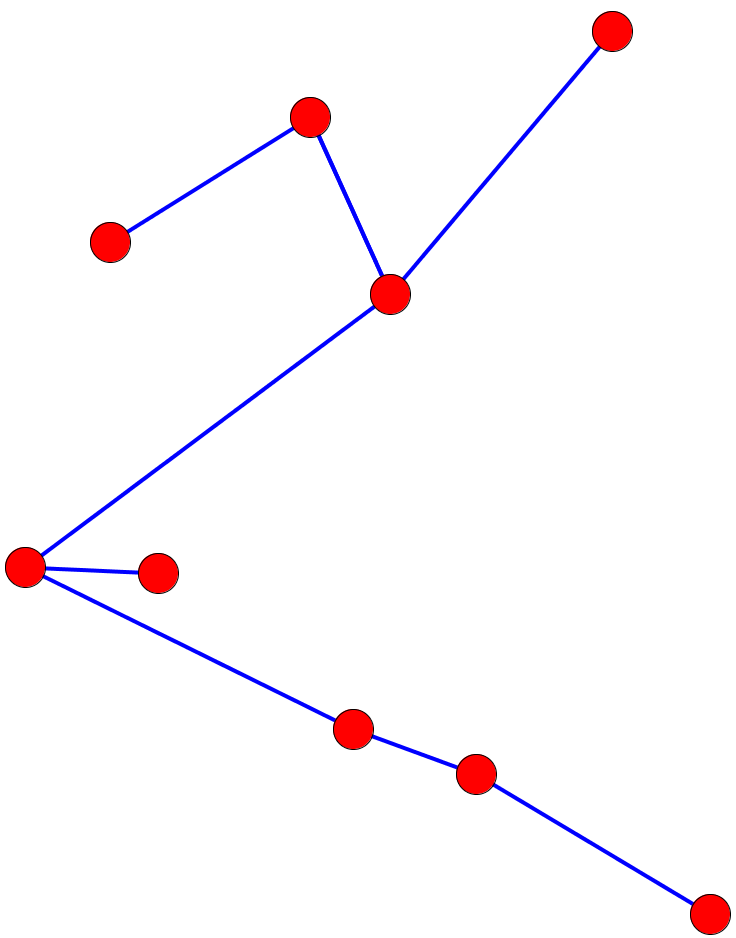
Un arbre est un graphe connexe, acyclique et non orienté.
En plaçant un point sur chaque cellule de notre labyrinthe, et en reliant deux cellules séparées par une porte, on peut dessiner un arbre à partir de n'importe quel labyrinthe.
Génération
Un labyrinthe rectangulaire de largeur et de hauteur contient exactement portes.
Du point de vue du graphe, il y a donc arêtes.
Maintenant, comment répartir toutes ces portes de façon à ce que toutes les cellules soient accessibles et qu'il n'existe qu'un unique chemin entre l'entrée et la sortie ?
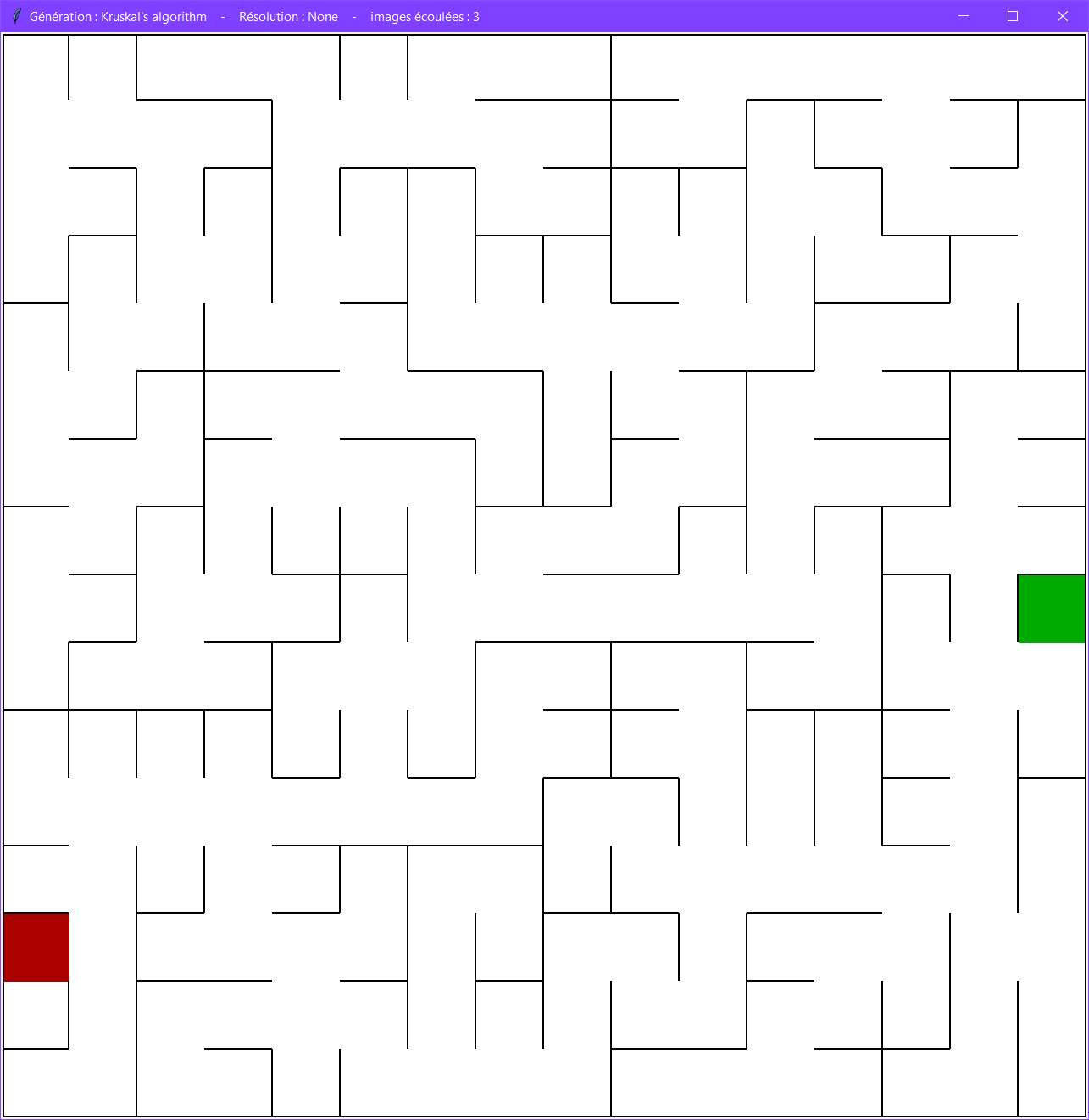
De nombreux algorithmes existent, dont le parcours en profondeur et l'algorithme de Kruskal. Chaque algorithme est différent et produit des labyrinthes visuellement différents.
En effet, si nous comparons un labyrinthe généré avec l'algorithme du parcours en profondeur à un labyrinthe généré avec l'algorithme de Kruskal, bien qu'ils aient tous les deux une solution unique, ils apparaissent néanmoins différents visuellement.
Parcours en profondeur
Dans l'algorithme du parcours en profondeur ("recursive backtracker" en anglais), on commence sur une cellule aléatoire dans le labyrinthe.
On se dirige dans une direction aléatoire et on casse le mur en face, tout en marquant la cellule précédente comme visitée.
Lorsque aucune direction n'est disponible, on remonte à la position précédente.
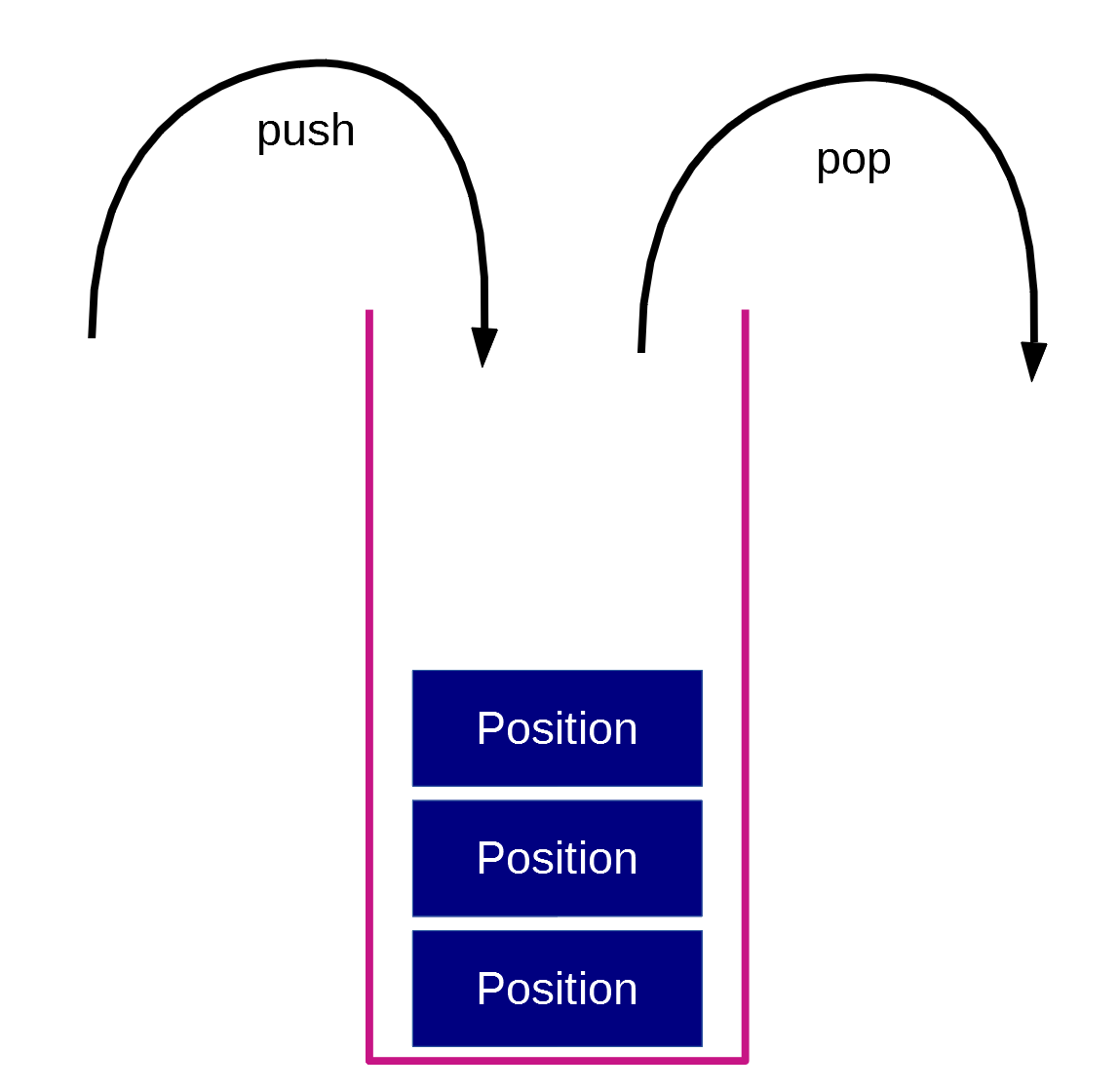
Pour sauvegarder l'historique des positions, on peut utiliser une pile.
Une pile est une liste dans laquelle seul le dernier élément peut être récupéré.
Une pile contient 2 méthodes :
- push(elem) : ajoute elem à la pile
- pop() -> elem : retourne le dernier élément de la pile (elem dans notre cas)
Dans mon implémentation de la pile, une erreur est levée si l'on appelle la méthode pop sur une pile vide.
Kruskal
Alors que pour le parcours en profondeur on partait des cellules, l'algorithme de Kruskal s'applique sur des murs.
On attribue à chaque cellule un identifiant unique.
On choisit un mur aléatoire. Si les cellules séparées par ce mur ont des identifiants différents, on leur associe le même identifiant et on casse le mur.
Sinon, on passe à un autre mur.
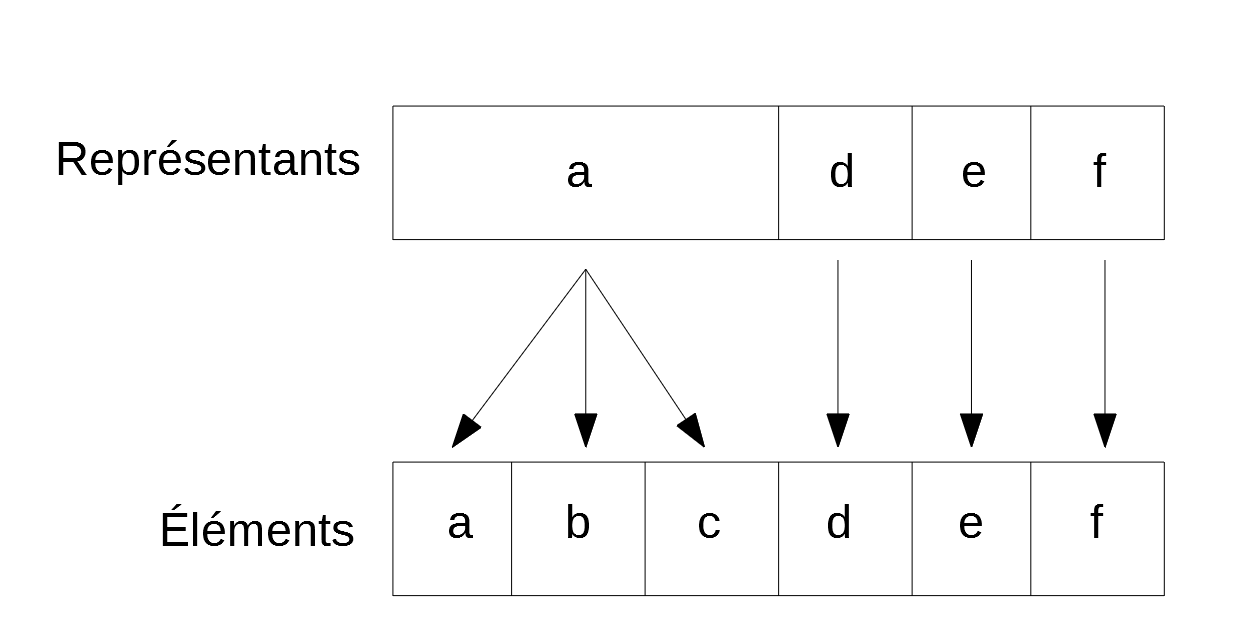
Pour mettre en œuvre cet algorithme, on utilise une structure de données appelée Union-Find, qui permet de mettre en relation des éléments partageant un même représentant (ou un même identifiant).
Il existe plusieurs variantes d'Union-Find, dont notamment la compression de chemin, qui permet de n'avoir qu'un ou deux éléments à parcourir pour obtenir le représentant d'un élément.
Union-Find fonctionne comme un arbre. a un représentant , etc..., qui lui même a un représentant , qui est son propre représentant.
Union-Find est composé de deux méthodes :
- union(a, b) : associe à et le même représentant, par exemple le représentant de
- find(a) -> : tant que l'élément n'est pas son propre représentant, on applique find au représentant de l'élément.
On commence donc par find(a), puis find(A) (si est le représentant de ), etc... La méthode de la compression de chemin permet d'éviter trop de récursivité en écrivant : représentant de :=
Labyrinthes cycliques
Il est possible, en retirant un certain pourcentage de murs, de créer des labyrinthes cycliques à partir des labyrinthes acycliques générés auparavant.
Cependant, certains algorithmes de résolution n'adopteront pas le même comportement.
Résolution
Il existe là encore de nombreux algorithmes de résolution de labyrinthes, plus ou moins efficaces, et surtout ne fonctionnant pas tous dans les mêmes conditions.
Parcours en profondeur
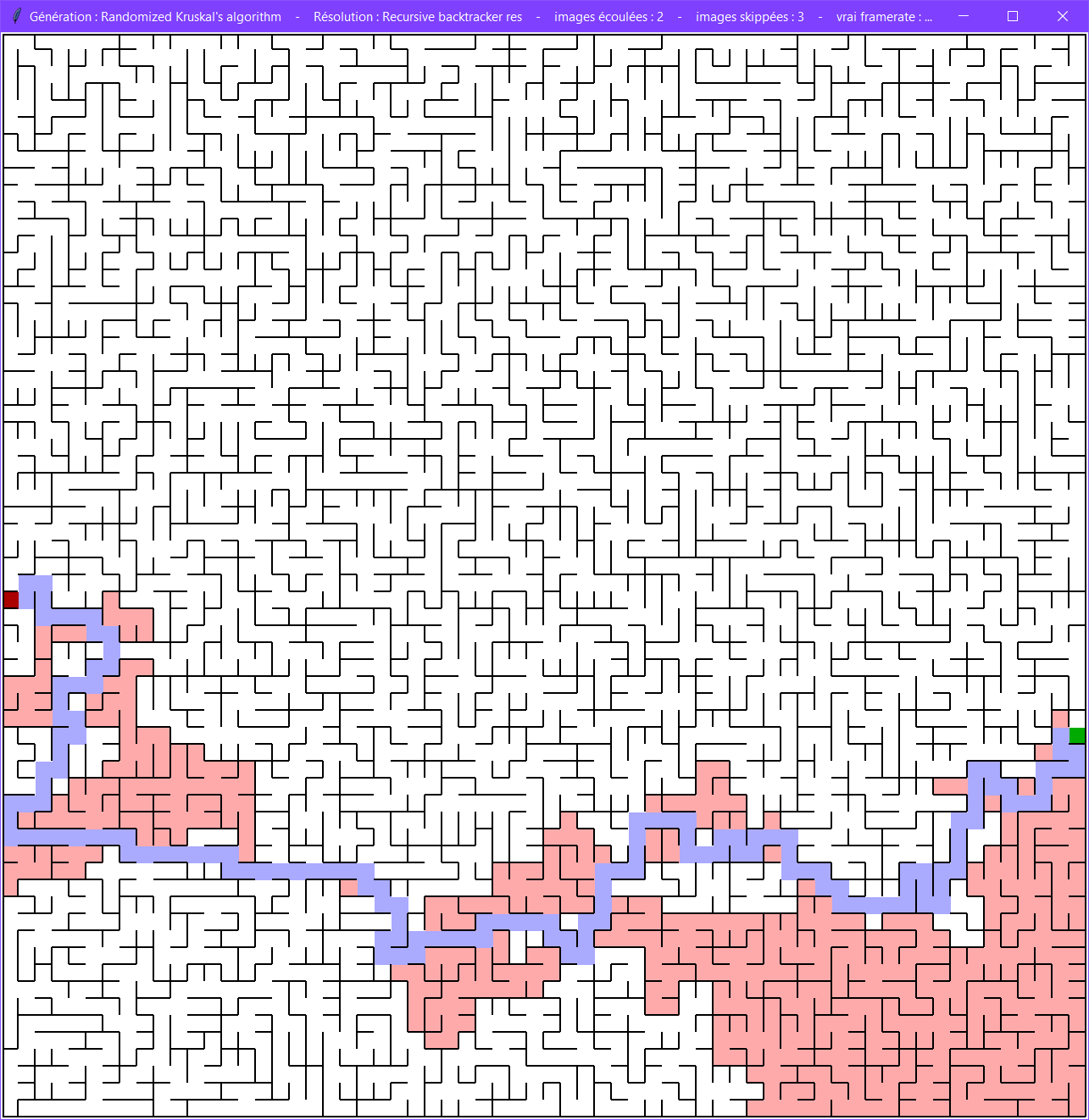
Cet algorithme est quasiment identique à celui du parcours en profondeur pour la génération.
Il est très efficace et trouvera une solution en minimisant le nombre de cases visitées.
Il s'adapte aux labyrinthes cycliques. En cas de boucle, il ne fera pas la boucle vu que l'intersection a déjà été visitées, il reviendra sur ses pas.
Il s'adapte aux labyrinthes sans solution. En effet, s'il n'y a pas de sortie, il va revenir à sa position de départ sans position précédente (pile vide) et en ayant parcouru toutes les cases.
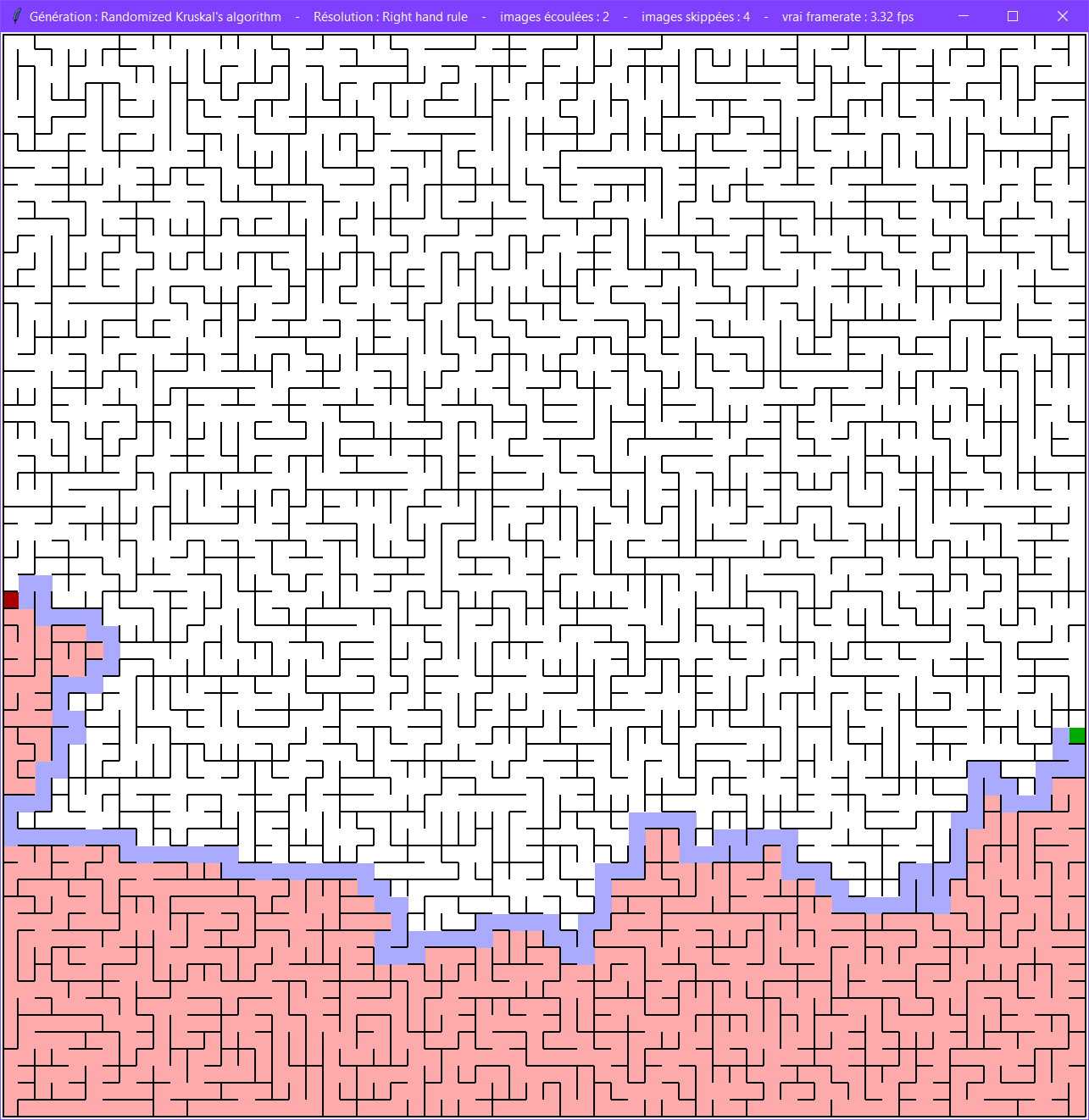
Mur droit
Cet algorithme va suivre de la main droite le mur de droite.
Il est relativement inefficace, et va visiter un grand nombre de cases.
Il s'adapte assez mal aux labyrinthes cycliques. En effet, si la sortie n'est pas dans la même boucle que l'entrée, il ne la trouvera jamais.
Il ne s'adapte pas aux labyrinthes sans solution, et fera le tour de la grille à l'infini.
Code source
Mon projet total contenant plusieurs milliers de lignes de code réparties dans une dizaine de fichiers, je ne peux évidemment pas l'insérer directement dans cette page.
Le code source est disponible sur Github à cette adresse
Il suffit d'avoir installé Python 3 et tkinter.
Sources
Génération
Résolution
Structures de données
Python