Apprentissage automatique

L'objectif de ce projet était de se familiariser et de comprendre l'apprentissage automatique, plus communément appelé Deep Learning. Pour ceci, il faut premièrement définir ce qu'est un neurone (en informatique) et donc un réseau de neurones. On parlera ensuite de la façon dont ces systèmes s'adaptent d'eux même, et comment on peut réduire la vitesse d'amélioration pour obtenir un bon programme.

Deep Learning

Le Deep Learning est le procédé par lequel un programme va apprendre lui même tout au long de son fonctionnement, mais plus particulièrement durant une période appelé le "training", l'entraînement en français. Durant cette période, on donne au programme des échantillons d'entraînement, qui contiennent la réponse que devrait donner le programme pour que celui-ci s'adapte en fonction de ses erreurs. À la fin, le programme possède un pourcentage de réussite qui définit sa fiabilité par la suite.

Neurones

Pour que cet apprentissage ait lieu, il faut un support à améliorer. Ce support ne sont d'autres que des neurones:

Perceptrons

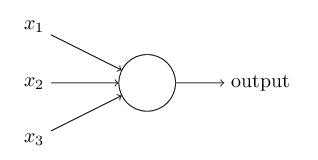
Ce type de neurone créé dans les années 50 a un fonctionnement simple. En effet, le neurone prend plusieurs entrées binaire (0 ou 1) pour donner une sortie binaire.

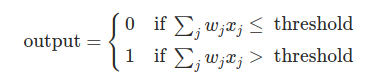
Comme le montre les inéquations ci dessus, chaque entrée possède un poids qui donne son importance. Si la somme du produit de chaque entrée et de son poids est supérieur à une valeur seuil alors le neurone donne un 1 sinon il donne un 0. Nous pouvons aussi interpréter ces inéquations, en faisant entrer en jeu le biais noté b qui va être en quelque sorte la difficulté pour que le perceptron retourne un 1.

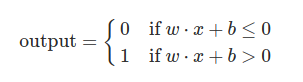
Pour améliorer le jugement d'un perceptron, il faut donc faire varier le poids et le biais de chaque entrée afin de retourner le bit qu'il doit donner.

Les neurones sigmoïdes

Un majeur problème du perceptron est qu'un faible changement des poids et des biais peu résulter en un changement total du résultats, nous éloignant fortement du résultat attendu. Nous voulons qu'un petit changement nous rapproche encore plus du résultat parfait quoi qu'il arrive pour éviter les erreurs et ne nous mène pas vers un résultat complètement différent.
Le neurone sigmoïde est fait pour éviter ses problème, en effet comme le perceptron il possède un poids et un biais par entrée cependant sa sortie n'est pas 0 ou 1 mais σ(w⋅x+b) où

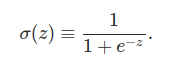
Si z est positif et très grand alors σ(z) est environ égal à 1, si z est négatif et très petit alors σ(z) est environ égale à 0. Dans les extrêmes le neurone sigmoïde se comporte tout comme un perceptron. La différence est visible quand w⋅x+b est un nombre de taille raisonnable, la sortie n'étant plus 0 ou 1 mais un flottant compris entre 0 et 1. On peut voir cela sur la courbe de la fonction :

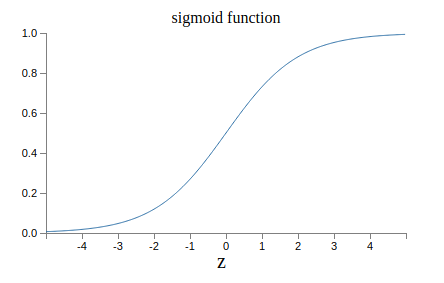
Le neurone sigmoïde est donc bien plus précis que le perceptron évitant les dérivations du résultat.