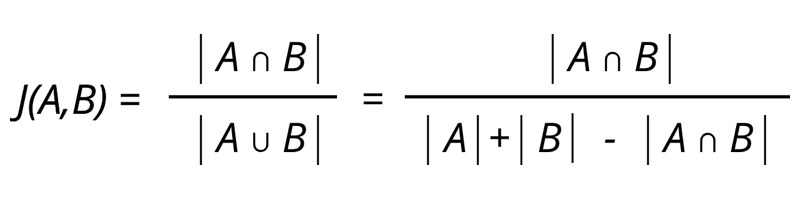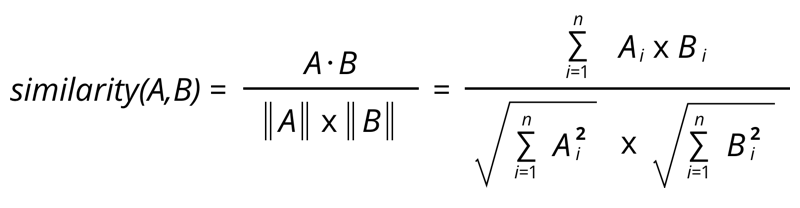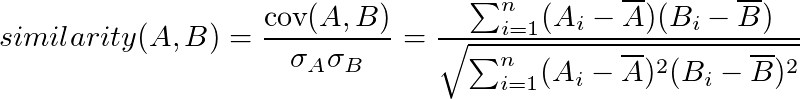Base de données orientées Graphe, similarité et recommandation
Aujourd'hui les base de données sont partout, avec la quantité d'information a stocké il a fallu inventer des moyen de les stocker. Au début il y avait des bases de données relationnels qui pouvait stocker de l'information en grande quantité mais ne permettait pas de gérer les relations entre les éléments de la base. C'est pour cela que les base de données orientées graphes ont vu le jour.
Les bases de données orientées graphes :
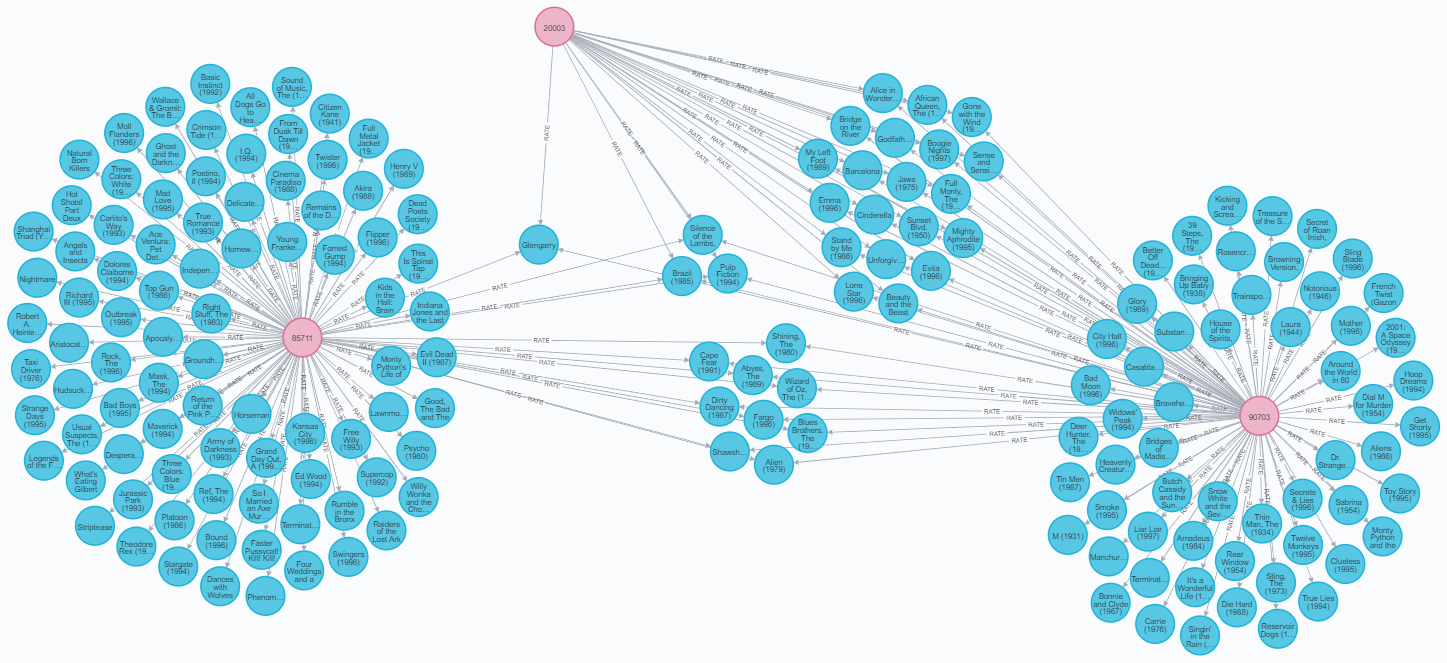
Les base de données orientées graphes peuvent stocker des éléments comme des individus ou des objets, mais également les relations entres les éléments. Les éléments sont ce qu'on appel des nœuds, et les liens des arêtes. On les représentent comme ceci :
On voit ici différents nœuds représentés par des cercle de couleur, et leur lien par des flèches les reliant. Chaque nœud peut avoir des données personnels, ici ce sont des individus en rose qui ont un nom, un métier, un genre etc... Idem pour les nœuds bleu qui représentent des films qui ont un titre, un genre, une date etc...
Cette représentation permet d'avoir un effet très visuel pour analyser les informations de ces bases. On va ainsi pouvoir rapprocher les liens en créant des chemins. En effet avec tous ces liens ont peut facilement relié les éléments entre eux en parcourant une série de lien, ce qu'on va appeler un chemin. Par exemple sur l'image ci-dessus on voit que les individus de gauche et de droite sont relié par des films qu'ils ont en commun, ainsi on peut les relié soit directement soit à l'aide d'un utilisateur intermédiaire.
Système de recommandation :
Avec le grand nombre d'information et de choix qui nous sont offert aujourd'hui, il est difficile de faire des choix, trop d'information nous empêche de faire un choix implicite car il nous est impossible de tout regarder. C'est pourquoi la recommandation est très présente de nos jours, elle compare un nombre énorme d'information pour sortir un choix qui n'est pas évident à voir.
Pour cela on peut se servir des base de données orientés graphes pour rapprocher les individus selon leur ressemblance et ainsi obtenir des elements recommandable. Pour tester cette ressemblance nous allons utiliser des algorithmes de similarités. Trois algorithmes ont été vus lors de ce projet :
La similarité de Jaccard
Elle consiste en la comparaison des éléments partagés de 2 individus. L’indice de Jaccard va de 0 pour aucune similarité a 1 pour une similarité très grande. Cet indice s’obtient en faisant le quotient de l’intersection des éléments des 2 individus, ce qu’ils ont en commun, sur l’ensemble des éléments des 2 individus. Cet indice permet de voir la similarité entre 2 personne mais ne prend pas en compte l’avis des individus, leur lien entre les éléments peut être positif comme négatif, ce que Jaccard ne prend pas en compte.
Soit 2 ensembles des liens, la formule s'obtient donc par le quotient des éléments partagés par les deux ensembles sur tous les éléments des ensembles.
La similarité Cosinus
Elle consiste en la comparaison des avis des individus, en effet les liens peuvent être pondérés, cela permet de prendre en compte les avis des individus sur leur lien. L’indice peut donc aller de -1 à 1, -1 signifiant une similarité opposée, 0 pour aucune similarité, et 1 pour une similarité parfaite. Cette méthode possède quand même ces inconvénients, en effet elle ne prend pas en compte l’échelle des avis. Pour un individu, une certaine note ne correspondra pas forcement à la même note pour un autre individu alors que le ressenti est le même.
La formule s'obtient en se basant sur les mathématique en voyant les ensemble des liens pondérés comme des vecteurs. On a donc le quotient du produit scalaire des 2 vecteurs sur le produit des normes des deux vecteurs
La similarité de Pearson
La similarité de Pearson se base sur les statistiques. A l’aide de la covariance et de l’écart à la moyenne, on obtient une similarité qui prend en compte les valeurs des liens. Grace à cette notion de moyenne on enleve ce problème d'echelle de la similarité cosinus et on obtient ainsi un similarité de tendance.
La formule s'obtient en faisant le quotient de la covariance entre 2 ensemble sur la somme des leur ecart type.