Tables de hachage et dictionnaires

Les tables de hachages sont des tableaux dynamiques permettant de créer une association clé-valeur pour une retrouver rapidement une valeur. Les codes proposés ici pour les tables et fonctions de hachages sont écrits en langage Python. Les dictionnaires Python sont également basés sur le principe des tables de hachage et serviront d’outil de comparaison.

Définitions

• Table de hachage : tableau associatif permettant de créer une association clé-valeur. Chaque couple ou valeur se voit attribuer une position dans la table à l’aide d’un entier, appelé valeur de hachage, renvoyé par une fonction de hachage. Cette position dépend de la taille de la table et non de l’ordre d’arrivée. La recherche ou modification d’une valeur, la suppression ou l’ajout d’un couple s’effectuent à l’aide de la clé, elle apparaît donc de façon unique dans la table.
• Fonction de Hachage : fonction associant une valeur entière de taille prédéfinie à un entier, un flottant ou une chaine de caractères de taille non prédéfinie.

Fonction de Hachage

Première approche des fonctions de hachage

Une fonction de hachage prend en paramètre un élément ‘hachable’, c’est-à-dire un élément immuable, en python ce sont les chaines de caractères, un entier, un flottant ou encore un tuple. Le but est de transformer cet élément en un nombre entier de taille définie pour ensuite qu’il devienne un indice correspondant à une position dans la table de hachage.

Réduire des éléments de taille non définie en entier de taille définie risque de causer des collisions, c’est-à-dire qu’au moins deux éléments obtiennent le même résultat. Or selon le format des tables, ces éléments ne peuvent pas occuper la même position (2.3). Ce problème est inévitable lorsque les ajouts d’éléments ne sont pas prédictibles. Le mieux est donc de limiter le nombre de collisions. Pour cela, il faut bien construire la fonction de hachage.

Exemple d'une mauvaise fonction de hachage

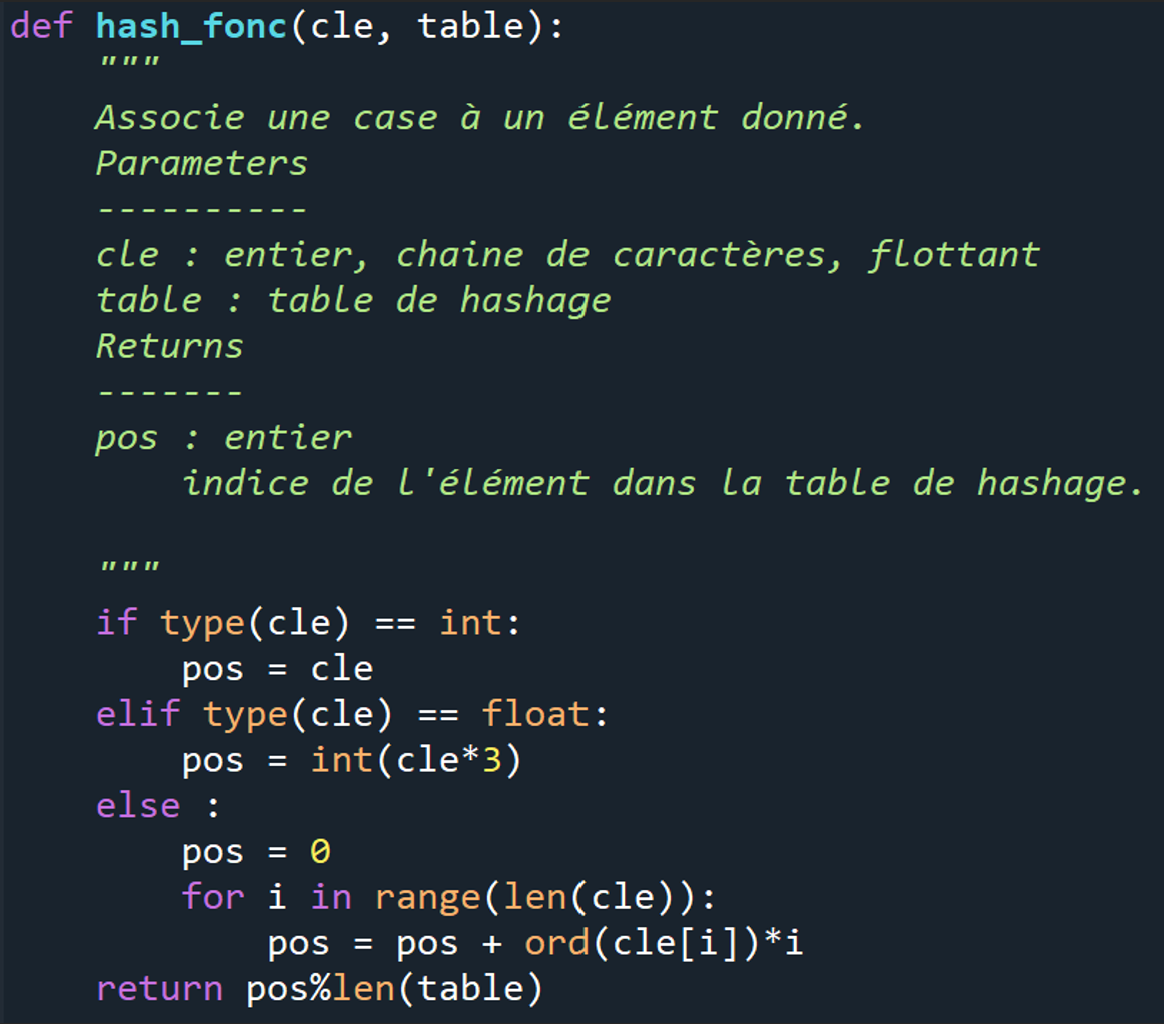
Par exemple la fonction ci-contre n’est pas une bonne fonction de hachage car :

• La table de hachage apparait dans la fonction, or la fonction de hachage doit en être indépendante.
• Le ‘else’ permet d’associer un entier à une chaine de caractère : l’indice est la somme de chaque caractère de la chaine transformée en son numéro ASCII puis multipliée par sa position dans la chaine. Ainsi, chaque premier caractère de chaine n’est pas pris en compte dans la somme (multiplication par 0) donc les chaines d’un caractère ont toutes pour indice 0 de la même façon, ‘mot’, ‘lot’, ‘got’ ont le même indice, etc…
• Pour ce qui est des entiers, tous les nombres entiers multiples de la taille de la table auront le même indice. La répartition des positions n’est pas suffisamment homogène.

Un autre exemple de fonction à éviter, est une fonction qui effectue une multiplication par un entier pair. Les cases occupées de la table se limiteraient alors aux indices pairs.

Ainsi, il est recommandé d’effectuer une multiplication par un grand nombre premier pour améliorer la répartition lors du modulo étant donné que les propriétés des nombres premiers sont utilisées. De la même façon, il est bien que le modulo final soit un nombre premier. Enfin, la réduction de l’indice à une position de la table se fera directement dans les méthodes de la table.

Différents types de fonctions

De nombreuses fonctions de hachage ont été imaginées pour répondre au mieux aux critères de répartition et de calcul.

Hachage multiplicatif

Exemple de décalages en base 10.
Le fonctionnement est similaire en base 2.

Le hachage multiplicatif consiste à prendre une clé m et la multiplier par une constante. Le modulo 1 conserve la partie fractionnaire seulement. Ce résultat est à nouveau multiplié par une puissance de 2 ce qui facilite les calculs pour l’ordinateur qui fonctionne avec des bits. En effet, une multiplication par n = 2p représente donc simplement un décalage p vers la droite. L’indice renvoyé est la partie entière de ce nombre.

Formule : $hash(m)=floor({n}\times {(({m}\times {c})mod1)})$ Avec m la clé, c une constante et n une puissance de 2.

Hachage de Fibonacci

Le hachage de Fibonacci est une variante du hachage multiplicatif. La constante c du hachage multiplicatif est à présent : ${\dfrac {2^{t}}{\phi }}$ avec t la taille de la clé et φ le nombre d’or : ${\dfrac {1+{\sqrt {5}}}{2}}$. Cette fonction renvoie des indices de manière uniforme sur l’ensemble de la table.

Fonction de hachage parfaite

Les fonctions précédentes limitent les collisions mais celles-ci sont toujours possible. La fonction de hachage parfaite a pour but de renvoyer de manière unique une valeur de hachage pour chaque clé. Il est possible d’en créer une lorsque les clés sont connues et que celles-ci ne risquent pas de changer. Pour les autres cas, une telle fonction est difficile à trouver en un temps de calcul raisonnable.

Table de Hachage et optimisation

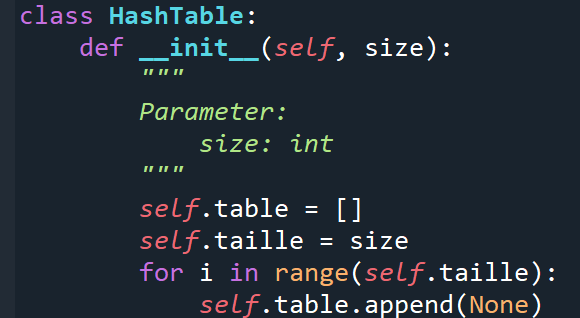
Les tables de hachage s’implémentent comme de simples tableaux de listes avec certaines propriétés. Il est possible de les initialiser avec la taille voulue. Ces tableaux peuvent être implémentés sous deux formes :

Hash 1	Hash 2
Tableau contenant une liste de tableaux	Tableau contenant une liste de valeurs par défaut (None)

Changement de taille de la table

La taille prédéfinie ne reste pas telle quelle selon les actions effectuées par l’utilisateur, on dit que ce sont des tableaux dynamiques.

Espace libre et ajout d’un élément

Les tables de hachage sont initialisées comme étant vide aux yeux de l’utilisateur. En réalité, la table possède déjà une taille positive non nulle. Dans les exemples ci-dessus, il est possible de choisir la taille initiale.

Taux d’agrandissement : 2
Espace vide : 1%
On remarque que le nombre de collisions est élevé par rapport au nombre d’éléments.

Il sera par moment nécessaire d’agrandir la table lorsqu’elle n’a plus de case vide (cf. Hash2) mais que l’insertion d’éléments n’est pas terminée, ou pour une meilleure gestion du nombre de collisions. Pour cela, il est bon de prévoir une marge de mémoire vide. Par exemple, une table initialisée à une taille de 4, avec une marge de 50% d’espace vide s’agrandira à l’ajout d’un troisième élément. Cette opération met en jeu deux paramètres : le pourcentage de mémoire vide et le taux d’agrandissement.

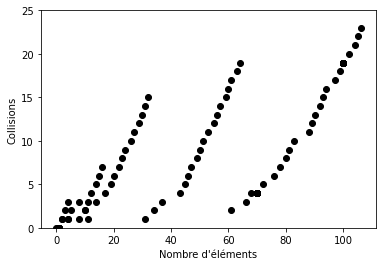
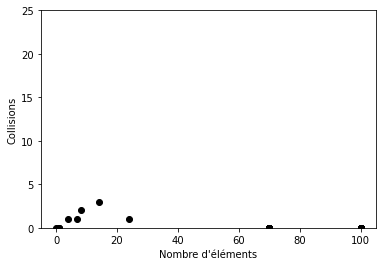
Tests complémentaires en Annexe 6.1. Après plusieurs tests en faisant varier la marge et l’augmentation de la taille, doubler la capacité de la table lorsque les deux tiers de sa taille sont occupés, est un compromis d’optimisation raisonnable. L’espace vide n’est pas gaspillé de manière excessive et le nombre de collisions n’est pas trop élevé.

Suppression d’un élément

De la même façon que l’ajout d’un élément, sa suppression s’effectue à partir de la clé donnée par l’utilisateur. La valeur de hachage est calculée et la complexité de la recherche est de $O(1)$ dans le meilleur des cas.

Lorsque l’élément est le seul à se trouver à l’emplacement indiqué, il n’y a pas de collision détectée au niveau de ce couple, dans le cas de hash 1, l’élément est supprimé du tableau pour retrouver un tableau vide. Dans le cas de hash 2, deux possibilités :

• Mettre une nouvelle valeur par défaut, par exemple -1,
• Mettre la valeur par défaut initiale : None.

Etapes de la suppression avec -1

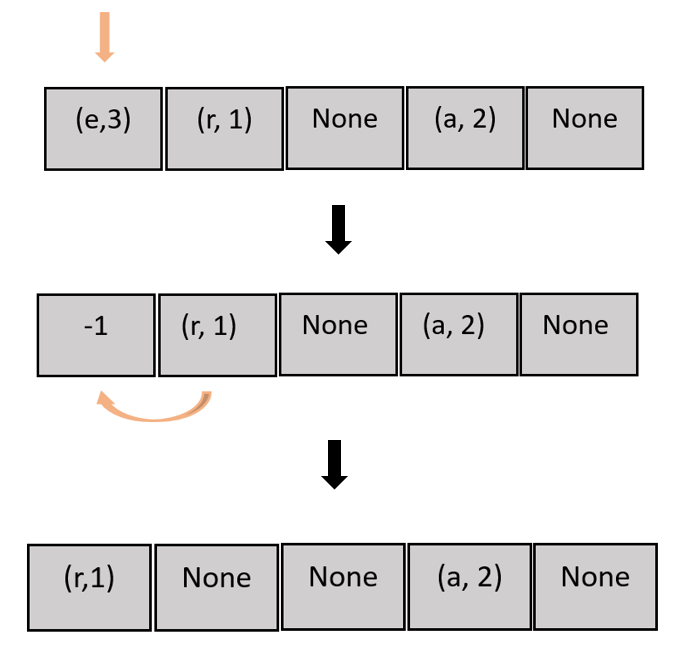
Cas du -1 :
Lorsque le couple à supprimer est trouvé, il est remplacé par la valeur « -1 ». Pour une recherche plus efficace, dès que le taux défini de « -1 » est atteint, il faut parcourir la table afin de retirer et replacer les éléments suivant leur valeur de hachage. En effet lorsque deux éléments sont en collisions, dans le cas de hash2, on insère l’élément dans la case vide suivante. Si le premier élément est supprimé, celui avec qui il était en collision doit récupérer sa place.

Cas du None :
A chaque suppression, l’élément est remplacé par sa valeur par défaut initiale : None. Puis, si une collision a été supprimée, alors les éléments dans la table sont replacés.

S’il est prévu un grand nombre d’insertions puis un grand nombre de suppressions, il peut être intéressant de réduire la taille de la table. Cependant si les insertions et suppressions sont nombreuses et répétitives, il est préférable de conserver la taille de la table lors du dernier agrandissement afin d’avoir un temps de calcul raisonnable.

Gestion des collisions

Adressage fermé

L’adressage fermé consiste à créer une chaine d’éléments de façon externe à la table. Pour le cas de Hash1, la table de hachage est un tableau de tableaux, ainsi il est possible d’insérer plusieurs couples au sein de chacun des sous-tableaux. La position des couples après la fonction de hachage est inchangée, il suffit de parcourir le sous-tableau pour le retrouver.

Adressage ouvert

Lors de collisions, avec une table comme Hash2, il est possible de placer l’élément en collision dans une autre que case que celle indiquée par la position.
Adressage ouvert linéaire : l’insertion s’effectue dans la prochaine case vide en parcourant la table de 1 en 1.
Adressage ouvert quadratique : le parcours des cases se fait de manière quadratique.
La formule est position = (hash(k) + f(x)) mod t, avec hash() la fonction de hachage, k la clé, f(x) une fonction et t la taille de la table. Par exemple :
Soit f(x) = x2 + 3x.
Une table de hachage :