Calcul des valeurs de Grundy pour des jeux octaux

Étudiant : Mathieu BRUNOT

Tuteur : Valenti Gledel

Jeu de Impartiaux

Description

Un jeu impartial est un jeu à 2 joueurs où les joueurs jouent à tour de rôle et leurs mouvements possibles ne dépendent pas du joueur qui joue, il n'y a donc pas de hasard ni d'égalité dans une partie.

Le perdant étant celui qui ne peut plus jouer, aussi appelé version normale.

En voici des exemples:

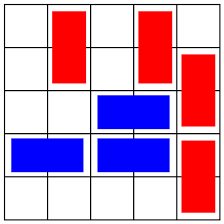
• Jeu de Cram
  Les joueurs mettent des dominos sur une grille. Le joueur qui met le dernier domino gagne.
  
• Jeu de Nim
  Il se joue avec un ou plusieurs tas d'objets exemple des allumettes.
  Chacun des joueurs joue à tour de rôle en choisissant un tas et en retirant autant d’allumettes que souhaité dans le tas, pour que son adversaire n’ait plus la possibilité de jouer, c’est ainsi que le jeu prend fin.
  
• Jeu des bâtonnets Fort Boyard
  Ce jeu consiste à n’avoir que le droit de retirer de 1 à 3 bâtonnets à chaque tour. Hormis la différence est que le joueur perdant est celui qui prend le dernier bâtonnet. Cette condition de victoire est appelé version misère.
  

Stratégie Gagnante

En effet, l’ensemble des jeux impartiaux sont résolubles à l’aide d’outils théorique afin de connaitre l'action à faire pour être le joueur en position gagnante.

Prenons le jeu de Fort Boyard mais cette fois-ci en version normale. Dans celui-ci la stratégie gagnante est de laisser un tas à l'adversaire qui serait un multiple de quatre.

• Pour le trouver il suffit de regarder les positions perdantes dans chaque cas:
  1. Si le nombre de bâtonnets est n=1, le joueur courant gagne car il peut enlever le dernier jeton et laisser l'adversaire avec un tas vide.
  2. Si n=2, le joueur courant gagne car il peut retirer les derniers bâtonnets.
  3. Si n=3, le joueur courant gagne car il peut retirer les derniers bâtonnets.
  4. Si n=4, le joueur courant perd car il va forcément laisser son adversaire dans une position gagnante.
  5. Plus généralement, toute position où $n\equiv 1,2,ou3{\pmod {4}}$est une position gagnante, et toute position où $n\equiv 0{\pmod {4}}$ est une position perdante.

Ainsi on pourrait se demander la stratégie gagnant d'autres jeux tel que le jeu de Nim ou le jeu de Cram

Valeurs de Grundy

Théorème de Sprague-Grundy

Le théorème de Sprague-Grundy nous permet de trouver la stratégie gagnante d’un jeu impartial fini en version normale (le perdant est le joueur ne pouvant plus jouer).

La valeur de Grundy ou d’un tas se calcule récursivement par ses règles :

- Un tas vide a pour valeur de Grundy 0.
- Le nombre Grundy d’une position non nulle est le plus petit entier positif ou nul qui n’est pas dans la liste des valeurs de Grundy des positions que l’on peut atteindre à partir de notre position.

Une position perdante d’un jeu celle qui donne une valeur de Grundy de 0.

Calcul des valeurs pour le jeu de Nim

Cas à 1 tas

La valeur de Grundy du jeu de Nim classique d’un tas de taille n (un entier) est celle du nombre de bâtonnets dans ce tas.

On l’explique car toutes les tailles de tas strictement inférieures à n sont atteignables à partir de celui-ci. Alors le minimum exclu(mex) des valeurs atteignables est n.

On appelle ce nombre précis dans le cas du jeu de Nim, un nimber.

Donc par exemple dans un tas de taille 9 du jeu Nim, on aurait une valeur de Grundy de 9, ceci est simple à comprendre.

Cas à plusieurs tas

Dans le cas de plusieurs tas, la valeur de Grundy de tous les jeux est le XOR de toutes les valeurs de Grundy de chaque tas.

Par exemple :

Voici un jeu de Nim composé de trois tas de bâtonnets:

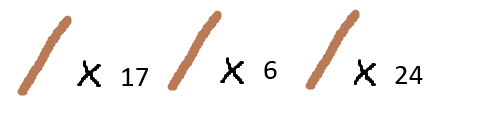
Ce jeu a pour valeur de Grundy : $17\oplus 6\oplus 24\Leftrightarrow 10001\oplus 00110\oplus 11000\Leftrightarrow 15$

Application

Mettons à l’œuvre nos connaissances afin de gagner une partie dans le jeu de Nim de l'exemple précédent.

Imaginons que nous soyons les premiers joueurs à jouer.

Nous nous trouvons dans une position gagnante car la valeur de Grundy du Jeu est de $15\neq 0$.

Pour pouvoir ramener celui-ci à une valeur de 0 pour que notre adversaire soit dans une position perdante, il nous suffit de changer un tas où la valeur de grundy de celui-ci possède un bit à 1 au même indice que le bit à 1 avec le plus grand exposant de 2 de la valeur de Grundy du jeu.

Dans notre cas le premier bit à 1 de 15 est celui qui est au 3eme exposant de 2. Le nombre qu’on doit changer est 24. Pour savoir à quelle valeur on doit le baisser il suffit de faire le XOR de 24 et de la valeur de Grundy du jeu qui est 15. On obtient $24\oplus 15=23$.

• On a choisi de retirer 1 bâton au tas de 24 pour avoir une valeur de Grundy totale de 0.
• L'adversaire est dans une position perdante, quoiqu’il fasse il ne peut pas passer en position gagnante.
• Il nous reste plus qu'à continuer ainsi pour s'assurer de gagner.

Jeux Octaux

Les jeux octaux sont aussi des jeux impartiaux, assez proches du jeu de Nim. Ils se jouent aussi avec des tas d’objet. Leurs caractéristiques sont que les coups autorisés sont définis à l’aide d’un système numérique de 0 à 7 d’où le nom jeu octal.

Règles

Les règles d'un jeu octal précisent les actions possibles lorsqu'un joueur retire n objets d'un tas donné, et sont encodées par une suite de chiffres entre 0 et 7 (d'où le nom jeu octal) :

Notation 0.k₁ k₂ k₃ k₄ …

où chaque chiffre k_n indique en combien de tas le joueur doit scinder le tas dans lequel il a retiré n objets. Le chiffre k_n est la somme de :

• $2^{0}$ si le joueur peut laisser 0 tas, 0 sinon;
• $2^{1}$ si le joueur peut laisser 1 tas, 0 sinon;
• $2^{2}$ si le joueur peut laisser 2 tas, 0 sinon

Par exemple, si k_n=0, les joueurs n'ont pas le droit de retirer n objets d'un tas. Si k_n=3, on retrouve la règle classique du jeu de Nim, à savoir que le joueur peut retirer n objets d'un tas de taille supérieure ou égale n.

Représentation en jeu octal

Comme vous l'avez compris il y a une infinité de jeux octaux.

On retrouve les jeux qu'on a introduit dans ces catégories. Jeu de Fort Boyard = 0.333
Jeu de Fort Boyard = 0.333